题目内容
若方程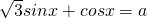 在[0.2π]上有两个不同的实数解,则a的取值范围是
在[0.2π]上有两个不同的实数解,则a的取值范围是
- A.a∈(-2,0)∪(1,2)
- B.a∈(-2,2)
- C.a∈(-2,1)∪(1,2)
- D.a∈(-2,1)
C
分析:已知方程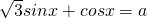 在[0.2π]上有两个不同的实数解,可以将方程转化为:sin(x+
在[0.2π]上有两个不同的实数解,可以将方程转化为:sin(x+ )=
)= ,可以令f(x)=sin(x+
,可以令f(x)=sin(x+ ),h(x)=
),h(x)= ,画出这两个函数的图象,利用数形结合的方法进行求解;
,画出这两个函数的图象,利用数形结合的方法进行求解;
解答:∵方程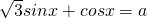 ,
,
∴2sinx(x+ )=a,即sinx(x+
)=a,即sinx(x+ )=
)= ,
,
可以令f(x)=sinx(x+ ),h(x)=
),h(x)= ,
,
∵方程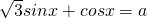 在[0.2π]上有两个不同的实数解,
在[0.2π]上有两个不同的实数解,
∴函数f(x)和h(x)的图象有两个交点,
如下图:
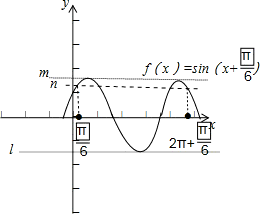
∴ ≤x+
≤x+ ≤2π+
≤2π+
∴h(x)= ,要使f(x)与h(x)有两个交点,
,要使f(x)与h(x)有两个交点,
∴h(x)在直线m与n和直线n与l之间,有两个交点,
∴ <
< <1或-1<
<1或-1< <
< ,
,
∴1<a<2或-2<a<1;
故选C;
点评:本题主要考查函数的零点及函数的零点存在性定理,函数的零点的研究就可转化为相应方程根的问题,数形结合的思想得到了很好的体现.
分析:已知方程
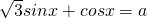 在[0.2π]上有两个不同的实数解,可以将方程转化为:sin(x+
在[0.2π]上有两个不同的实数解,可以将方程转化为:sin(x+ )=
)= ,可以令f(x)=sin(x+
,可以令f(x)=sin(x+ ),h(x)=
),h(x)= ,画出这两个函数的图象,利用数形结合的方法进行求解;
,画出这两个函数的图象,利用数形结合的方法进行求解;解答:∵方程
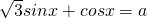 ,
,∴2sinx(x+
 )=a,即sinx(x+
)=a,即sinx(x+ )=
)= ,
,可以令f(x)=sinx(x+
 ),h(x)=
),h(x)= ,
,∵方程
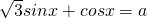 在[0.2π]上有两个不同的实数解,
在[0.2π]上有两个不同的实数解,∴函数f(x)和h(x)的图象有两个交点,
如下图:

∴
 ≤x+
≤x+ ≤2π+
≤2π+
∴h(x)=
 ,要使f(x)与h(x)有两个交点,
,要使f(x)与h(x)有两个交点,∴h(x)在直线m与n和直线n与l之间,有两个交点,
∴
 <
< <1或-1<
<1或-1< <
< ,
,∴1<a<2或-2<a<1;
故选C;
点评:本题主要考查函数的零点及函数的零点存在性定理,函数的零点的研究就可转化为相应方程根的问题,数形结合的思想得到了很好的体现.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 在(0, 2)内恰有一解, 则实数
在(0, 2)内恰有一解, 则实数 的取值范围为 .
的取值范围为 .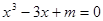 在[0,2]上有解,则实数m的取值范围为
( )
在[0,2]上有解,则实数m的取值范围为
( ) B.
B.  C.
C.
 D.
D.

 ,则方程
,则方程 在(0,2)上恰好有( )个根
在(0,2)上恰好有( )个根 在[0.2π]上有两个不同的实数解,则a的取值范围是( )
在[0.2π]上有两个不同的实数解,则a的取值范围是( )