题目内容
(1)
(2)已知
 ,求f(x)的解析式
,求f(x)的解析式(3)若二次函数y=ax2+bx+c的图象与x轴交于A(-2,0),B(4,0),且函数的最大值为9,求这个二次函数的表达式.
【答案】分析:(1)原式= =
=
(2)设 ,则t≥1,
,则t≥1, ,f(t)=(t-1)2+2(t-1)=t2-1,由此能求出f(x).
,f(t)=(t-1)2+2(t-1)=t2-1,由此能求出f(x).
(3)设y=a(x-x1)(x-x2),其中x1,x2是ax2+bx+c=0的两根,由y=ax2+bx+c的图象与x轴交于A(-2,0),B(4,0),知x1=-2,x2=4且函数图象的对称轴为x=1,又函数有最在值为9,故函数过(1,9),由此能求出这个二次函数的表达式.
解答:解:(1)原式=
=
=
(2)设 ,则t≥1,
,则t≥1, ,∴f(t)=(t-1)2+2(t-1)=t2-1
,∴f(t)=(t-1)2+2(t-1)=t2-1
所以f(x)=x2-1(x≥1)(没写x≥1扣1分)
(3)设y=a(x-x1)(x-x2),其中x1,x2是ax2+bx+c=0的两根,(2分)
∵y=ax2+bx+c的图象与x轴交于A(-2,0),B(4,0),(3分)
∴x1=-2,x2=4且函数图象的对称轴为x=1,(5分)
即有y=a(x+2)(x-4)(6分)
又函数有最在值为9,故函数过(1,9),(8分)
∴9=a(1+2)(1-4)⇒a=-1
∴y=-1(x+2)(x-4)=-x2+2x+8(10分)
点评:第(1)题考查对数的运算,解题时要注意对数性质和运算法则的灵活运用;第(2)题考查求解函数解析式的方法,解题时要注意换元法的灵活运用;第(3)题考查二次函数的图象和性质,解题时要注意抛物线性质的应用.
 =
=
(2)设
 ,则t≥1,
,则t≥1, ,f(t)=(t-1)2+2(t-1)=t2-1,由此能求出f(x).
,f(t)=(t-1)2+2(t-1)=t2-1,由此能求出f(x).(3)设y=a(x-x1)(x-x2),其中x1,x2是ax2+bx+c=0的两根,由y=ax2+bx+c的图象与x轴交于A(-2,0),B(4,0),知x1=-2,x2=4且函数图象的对称轴为x=1,又函数有最在值为9,故函数过(1,9),由此能求出这个二次函数的表达式.
解答:解:(1)原式=

=

=

(2)设
 ,则t≥1,
,则t≥1, ,∴f(t)=(t-1)2+2(t-1)=t2-1
,∴f(t)=(t-1)2+2(t-1)=t2-1所以f(x)=x2-1(x≥1)(没写x≥1扣1分)
(3)设y=a(x-x1)(x-x2),其中x1,x2是ax2+bx+c=0的两根,(2分)
∵y=ax2+bx+c的图象与x轴交于A(-2,0),B(4,0),(3分)
∴x1=-2,x2=4且函数图象的对称轴为x=1,(5分)
即有y=a(x+2)(x-4)(6分)
又函数有最在值为9,故函数过(1,9),(8分)
∴9=a(1+2)(1-4)⇒a=-1
∴y=-1(x+2)(x-4)=-x2+2x+8(10分)
点评:第(1)题考查对数的运算,解题时要注意对数性质和运算法则的灵活运用;第(2)题考查求解函数解析式的方法,解题时要注意换元法的灵活运用;第(3)题考查二次函数的图象和性质,解题时要注意抛物线性质的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目

 ,求
,求 的值.
的值. 
 ,求
,求 的值。
的值。 ;
;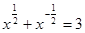 ,求
,求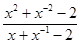 的值.
的值.
 ,求
,求 的值。
的值。