题目内容
△ABC中，BC=7，AC=3，∠A=120°，求以点B、C为焦点且过点A的椭圆方程．
解：由余弦定理得：BC2=AB2+AC2-2AB•AC•cos∠A（2分）
即49=AB2+9+3AB
得AB=-8（舍去）或 AB=5（4分）
以BC为x轴，BC垂直平分线为y轴建立直角坐标系 （6分）
由椭圆定义知2a=AB+AC=8，2c=BC=7（8分）
知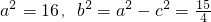
（10分）
故椭圆方程为
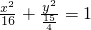（12分）
分析：解：由余弦定理得：得AB，以BC为x轴，BC垂直平分线为y轴建立直角坐标系，由椭圆定义，求出a，b值，从而求椭圆C的方程．
点评：本题主要考查了椭圆的标准方程问题．解答关键是利用坐标法解决问题．
即49=AB2+9+3AB
得AB=-8（舍去）或 AB=5（4分）
以BC为x轴，BC垂直平分线为y轴建立直角坐标系 （6分）
由椭圆定义知2a=AB+AC=8，2c=BC=7（8分）
知
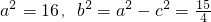（10分）故椭圆方程为
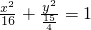（12分）分析：解：由余弦定理得：得AB，以BC为x轴，BC垂直平分线为y轴建立直角坐标系，由椭圆定义，求出a，b值，从而求椭圆C的方程．
点评：本题主要考查了椭圆的标准方程问题．解答关键是利用坐标法解决问题．
练习册系列答案
相关题目
．
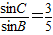