Question

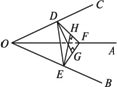
已知∠AOB＝60°，过点O引∠AOB所在平面的斜线OC与OA、OB均成60°，求二面角A－OC－B的平面角的正弦值．

Answer 1

答案：
解析：

解：如下图，在OC上任取一点D，在平面COB内作DE⊥OC交OB于E，在平面AOC内作DF⊥OC交OA于F， 　　 　　思路分析：本题考查利用二面角的平面角的定义求二面角大小的方法，由于OA、OB、OC均为射线，二面角的平面角的顶点无论取在何处，均能与已知条件取得联系． 　　温馨提示：根据二面角的平面角的定义直接作出二面角的平面角是最基本和最常用的方法之一，即过棱上任意一点分别在两个半平面内作棱的垂线，所得的角就是二面角的平面角．