题目内容
已知:函数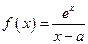 (其中常数
(其中常数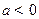 ).
).
(Ⅰ)求函数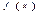 的单调区间;
的单调区间;
(Ⅱ)若存在实数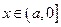 ,使得不等式
,使得不等式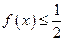 成立,求a的取值范围.
成立,求a的取值范围.
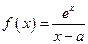 (其中常数
(其中常数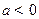 ).
).(Ⅰ)求函数
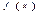 的单调区间;
的单调区间;(Ⅱ)若存在实数
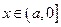 ,使得不等式
,使得不等式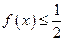 成立,求a的取值范围.
成立,求a的取值范围.(1)
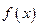 的单调递增区间为
的单调递增区间为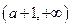 ,单调递减区间为
,单调递减区间为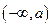 ,
,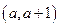
(2)
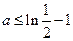
解:(Ⅰ)函数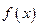 的定义域为
的定义域为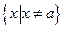 . ……………1分
. ……………1分
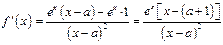 . …………………3分
. …………………3分
由
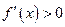 ,解得
,解得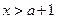 .由
.由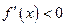 ,解得
,解得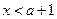 且
且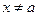 .
.
∴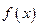 的单调递增区间为
的单调递增区间为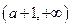 ,单调递减区间为
,单调递减区间为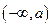 ,
,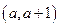 . 4分
. 4分
(Ⅱ)由题意可知,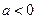 ,且
,且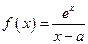 在
在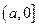 上的最小值小于等于
上的最小值小于等于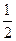 时,存在实数
时,存在实数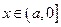 ,使得不等式
,使得不等式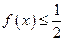 成立. ………6分
成立. ………6分
若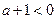 即
即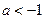 时,
时,
∴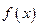 在
在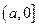 上的最小值为
上的最小值为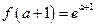 .则
.则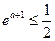 ,得
,得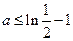 . …8分
. …8分
若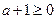 即
即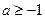 时,
时,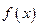 在
在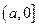 上单调递减,
上单调递减,
则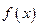 在
在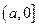 上的最小值为
上的最小值为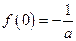 .由
.由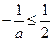 得
得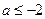 (舍). …10分
(舍). …10分
综上所述,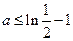 . ……………12分
. ……………12分
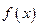 的定义域为
的定义域为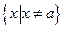 . ……………1分
. ……………1分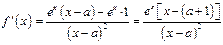 . …………………3分
. …………………3分由

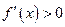 ,解得
,解得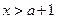 .由
.由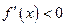 ,解得
,解得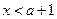 且
且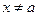 .
.∴
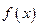 的单调递增区间为
的单调递增区间为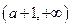 ,单调递减区间为
,单调递减区间为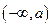 ,
,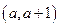 . 4分
. 4分(Ⅱ)由题意可知,
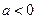 ,且
,且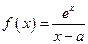 在
在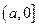 上的最小值小于等于
上的最小值小于等于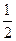 时,存在实数
时,存在实数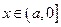 ,使得不等式
,使得不等式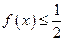 成立. ………6分
成立. ………6分若
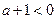 即
即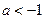 时,
时,| | X | 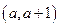 | a+1 | 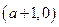 |
| | 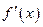 | - | 0 | + |
| | 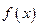 | ↘ | 极小值 | ↗ |
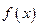 在
在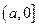 上的最小值为
上的最小值为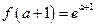 .则
.则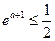 ,得
,得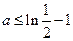 . …8分
. …8分若
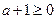 即
即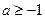 时,
时,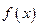 在
在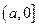 上单调递减,
上单调递减,则
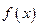 在
在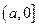 上的最小值为
上的最小值为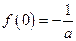 .由
.由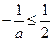 得
得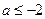 (舍). …10分
(舍). …10分综上所述,
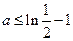 . ……………12分
. ……………12分
练习册系列答案
相关题目
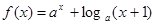 (
(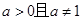 )在
)在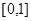 上的最大值与最小值之和为
上的最大值与最小值之和为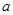 ,则
,则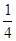
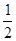
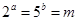 ,且
,且 ,则
,则 ( )
( )
 ,
, ,
,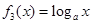 (其中
(其中 且
且 ),在同一坐标系中画出其中两个函数在x≥0且y≥0的范围内的大致图象,其中正确的是( )
),在同一坐标系中画出其中两个函数在x≥0且y≥0的范围内的大致图象,其中正确的是( )



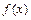 是定义在
是定义在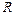 上的奇函数,当
上的奇函数,当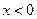 时,
时,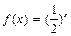 ,那么
,那么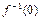 的值为( )
的值为( )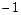
 ,
, 则
则 的取值范围是 ______
的取值范围是 ______ 的图象与直线
的图象与直线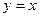 图象相切,则
图象相切,则
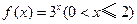 的值域为 ( )
的值域为 ( )



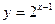 的反函
的反函 数是
数是


