题目内容
三个女生和四个男生排成一排.(1)如果女生必须全排在一起,有多少种不同的排法?
(2)如果女生必须全分开,有多少种不的排法?
(3)如果两端都不能排女生,有多少种不同的排法?
(4)如果两端不能都排女生,有多少种不同的排法?
(5)如果最高的站中间,两边均按从高到低排列,有多少种不同的排法?
(6)如果四个男同学按从高到低排列,有多少种不同的排法?
【答案】分析:(1)用捆绑法,分两步进行,先3名女生看为一个整体,再将其与4名男生进行全排列,分别求出其情况数目,进而由分步计数原理计算可得答案;
(2)用插空法,分两步进行,先将4名男生全排列,有5个空位,在5个空位中任选3个,安排3名女生,分别求出其情况数目,进而由分步计数原理计算可得答案;
(3)分两步进行,首先在4名男生中任取2人,安排在两端,再将剩余的5人安排在其他5个位置,分别求出其情况数目,进而由分步计数原理计算可得答案;
(4)用排除法,首先计算7人进行全排列的情况数目,再计算两端都站女生即先在3名女生中任取2人,再将剩余的5人安排在其他5个位置,的情况数目,用排除法即可得答案;
(5)只需将最高的人放在中间,在剩余的6人中任取3人放在左边,其他的3人放在右边,分析左右两边的顺序情况即可得答案;
(6)分两步进行,先在7个位置中安排3名女生,再将剩余4个位置安排4名男生,分别求出其情况数目,进而由分步计数原理计算可得答案.
解答:解:(1)根据题意,用捆绑法,3名女生看为一个整体,考虑其顺序有A33种情况,
再将其与4名男生进行全排列,有A55种情况,
则共有A55×A33=720种排法;
(2)用插空法,先将4名男生全排列,有A44种情况,
排好后,有5个空位,在其中任选3个,安排3名女生,有A53种情况,
则共有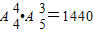 种排法;
种排法;
(3)在4名男生中任取2人,安排在两端,有2C42种情况,
再将剩余的5人安排在中间的5个位置,有A55种情况,
则共有2C42×A55=1440种排法;
(4)用排除法,
7人进行全排列,有A77种排法,
两端都站女生,即先在3名女生中任取2人,再将剩余的5人安排在其他5个位置,有A32•A55种站法,
则共有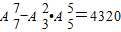 种排法;
种排法;
(5)只需将最高的人放在中间,在剩余的6人中任取3人放在左边,其他的3人放在右边,
由于顺序固定,则左右两边只有一种排法,
则有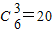 种排法;
种排法;
(6)先在7个位置中安排3名女生,有A73种排法,
剩余4个位置安排4名男生,有2种情况,
则有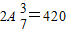 种排法.
种排法.
点评:本题考查排列、组合的运用,注意优先分析特殊位置、特殊元素;其次要掌握不相邻问题采用插空法,相邻问题采用捆绑法等常见问题的处理方法.
(2)用插空法,分两步进行,先将4名男生全排列,有5个空位,在5个空位中任选3个,安排3名女生,分别求出其情况数目,进而由分步计数原理计算可得答案;
(3)分两步进行,首先在4名男生中任取2人,安排在两端,再将剩余的5人安排在其他5个位置,分别求出其情况数目,进而由分步计数原理计算可得答案;
(4)用排除法,首先计算7人进行全排列的情况数目,再计算两端都站女生即先在3名女生中任取2人,再将剩余的5人安排在其他5个位置,的情况数目,用排除法即可得答案;
(5)只需将最高的人放在中间,在剩余的6人中任取3人放在左边,其他的3人放在右边,分析左右两边的顺序情况即可得答案;
(6)分两步进行,先在7个位置中安排3名女生,再将剩余4个位置安排4名男生,分别求出其情况数目,进而由分步计数原理计算可得答案.
解答:解:(1)根据题意,用捆绑法,3名女生看为一个整体,考虑其顺序有A33种情况,
再将其与4名男生进行全排列,有A55种情况,
则共有A55×A33=720种排法;
(2)用插空法,先将4名男生全排列,有A44种情况,
排好后,有5个空位,在其中任选3个,安排3名女生,有A53种情况,
则共有
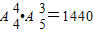 种排法;
种排法;(3)在4名男生中任取2人,安排在两端,有2C42种情况,
再将剩余的5人安排在中间的5个位置,有A55种情况,
则共有2C42×A55=1440种排法;
(4)用排除法,
7人进行全排列,有A77种排法,
两端都站女生,即先在3名女生中任取2人,再将剩余的5人安排在其他5个位置,有A32•A55种站法,
则共有
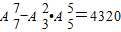 种排法;
种排法;(5)只需将最高的人放在中间,在剩余的6人中任取3人放在左边,其他的3人放在右边,
由于顺序固定,则左右两边只有一种排法,
则有
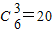 种排法;
种排法; (6)先在7个位置中安排3名女生,有A73种排法,
剩余4个位置安排4名男生,有2种情况,
则有
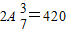 种排法.
种排法.点评:本题考查排列、组合的运用,注意优先分析特殊位置、特殊元素;其次要掌握不相邻问题采用插空法,相邻问题采用捆绑法等常见问题的处理方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则男生的编号之和小于女生编号之和的排法有 ▲
种.(请用数字作答)
,则男生的编号之和小于女生编号之和的排法有 ▲
种.(请用数字作答)