题目内容
 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(如图所示).(Ⅰ)根据图象,求一次函数y=kx+b的表达式;
(Ⅱ)设公司获得的利润(利润=销售总价-成本总价)为S元,写出S关于x的函数表达式,并求该公司可获得的最大利润.
分析:(Ⅰ)由图象知,当x=600时,y=400; 当x=700时,y=300,代入y=kx+b中,求得k和b的值,可得一次函数的解析式.
(Ⅱ)依题意得,S=xy-500y=-(x-750)2+62500(500≤x≤800),再利用二次函数的性质求得它的最大值
(Ⅱ)依题意得,S=xy-500y=-(x-750)2+62500(500≤x≤800),再利用二次函数的性质求得它的最大值
解答:解:(Ⅰ)由图象知,当x=600时,y=400; 当x=700时,y=300,
代入y=kx+b中,可得
,
解得
,
∴一次函数y=kx+b的表达式为 y=-x+1000(500≤x≤800).
(Ⅱ)依题意得,S=xy-500y=x(-x+1000)-500(-x+1000)=-x2+1500x-500000
=-(x-750)2+62500(500≤x≤800).
∴当x=750时,ymax=62500,即该公司可获得的最大利润是62500元.
代入y=kx+b中,可得
|
解得
|
∴一次函数y=kx+b的表达式为 y=-x+1000(500≤x≤800).
(Ⅱ)依题意得,S=xy-500y=x(-x+1000)-500(-x+1000)=-x2+1500x-500000
=-(x-750)2+62500(500≤x≤800).
∴当x=750时,ymax=62500,即该公司可获得的最大利润是62500元.
点评:本题主要考查用待定系数法求函数的解析式,求二次函数在闭区间上的最值,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.
某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.
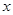 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数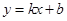 的关系(如下图所示).
的关系(如下图所示).
