题目内容
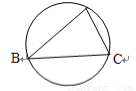
如图已知圆的半径为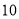 ,其内接
,其内接 的内角
的内角 分别为
分别为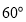 和
和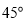 ,现向圆内随机撒一粒豆子,则豆子落在
,现向圆内随机撒一粒豆子,则豆子落在 内的概率为( )
内的概率为( )
A.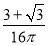 B.
B.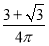 C.
C. D.
D.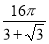
B
【解析】
试题分析:由正弦定理可得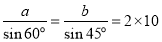 ,所以
,所以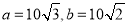 ,
,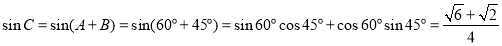 ,所以
,所以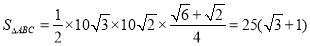 ,
,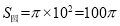 ,
,
所以所求概率为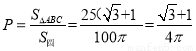 。故B正确。
。故B正确。
考点:几何概型概率公式。

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
题目内容
如图已知圆的半径为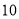 ,其内接
,其内接 的内角
的内角 分别为
分别为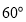 和
和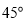 ,现向圆内随机撒一粒豆子,则豆子落在
,现向圆内随机撒一粒豆子,则豆子落在 内的概率为( )
内的概率为( )

A.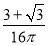 B.
B.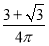 C.
C. D.
D.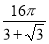
B
【解析】
试题分析:由正弦定理可得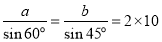 ,所以
,所以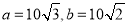 ,
,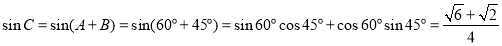 ,所以
,所以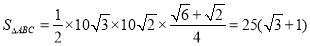 ,
,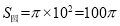 ,
,
所以所求概率为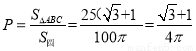 。故B正确。
。故B正确。
考点:几何概型概率公式。

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案