题目内容
设全集U=R,M={x|y=| x2-4 |
| 2 |
| x-1 |
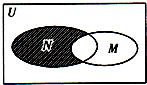
分析:先求出集合M与集合N,根据阴影部分所示的集合是N∩CUM,依据交集、补集的定义计算可得.
解答:解:M={x|x≤-2或x≥2},N={x|1<x≤3}
根据阴影部分所示的集合是N∩CUM,
则N∩CUM={x|1<x≤2},
故答案为{x|1<x≤2}.
根据阴影部分所示的集合是N∩CUM,
则N∩CUM={x|1<x≤2},
故答案为{x|1<x≤2}.
点评:本题考查了集合的运算,以及venn图表示集合的关系,属于基础题.

练习册系列答案
相关题目
设全集U=R,M={x|x>2},N={x|
<2},那么下列关系中正确的是( )
| 1 |
| x |
| A、M=N | |||||
B、M
| |||||
C、N
| |||||
| D、M∩N=φ |
设全集U=R,M={x|y=log2(-x)},N={x|
<0},则M∩?UN=( )
| 1 |
| x+1 |
| A、{x|x<0} |
| B、{x|0<x≤1} |
| C、{x|-1≤x<0} |
| D、{x|x>-1} |