题目内容
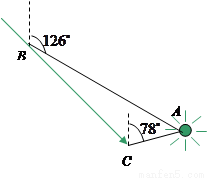
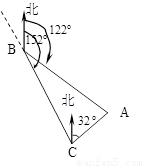
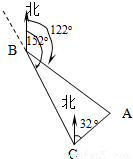
 如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122°.半小时后,货轮到达C点处,观测到灯塔A的方位角为32°.求此时货轮与灯塔之间的距离.
如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122°.半小时后,货轮到达C点处,观测到灯塔A的方位角为32°.求此时货轮与灯塔之间的距离.
分析:在△ABC中利用三角形内角和求得∠BCA和∠BAC,则BC可求得,最后利用正弦定理求得AC.
解答:解:在△ABC中,∠B=152°-122°=30°,∠C=180°-152°+32°=60°,∠A=180°-30°-60°=90°,…(4分)
BC=
,…(6分)∴AC=
sin30°=
.…(12分)
答:船与灯塔间的距离为
n mile.
BC=
| 35 |
| 2 |
| 35 |
| 2 |
| 35 |
| 4 |
答:船与灯塔间的距离为
| 35 |
| 4 |
点评:本题主要考查了解三角形的实际应用.解题的关键是建立三角函数的数学模型,运用三角函数的基础知识来解决实际问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
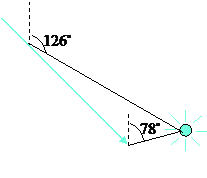
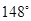 的方向航行.为了确定船位,在B点观察灯塔A的方位角是
的方向航行.为了确定船位,在B点观察灯塔A的方位角是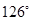 ,航行半小时后到达C点,观察灯塔A的方位角是
,航行半小时后到达C点,观察灯塔A的方位角是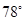 .求货轮到达C点时与灯塔A的距离(精确到1 n
mile).
.求货轮到达C点时与灯塔A的距离(精确到1 n
mile).