题目内容
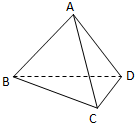 如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,
如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,(Ⅰ)求三棱锥A-BCD的体积;
(Ⅱ)求点A到BC的距离.
分析:(I)由已知中,用一付直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,我们利用面面垂直的性质,我们易求出三棱锥A-BCD的高AE的长,及底面△BCD的面积,代入棱锥体积公式,即可得到答案.
(II)过E点做EF∥CD,利用线面垂直的性质及判定定理,我们易判断AF即为点A到BC的距离,在RT△AEF中,求出AE及EF值后,利用勾股定理,我们易求出AF的值.
(II)过E点做EF∥CD,利用线面垂直的性质及判定定理,我们易判断AF即为点A到BC的距离,在RT△AEF中,求出AE及EF值后,利用勾股定理,我们易求出AF的值.
解答: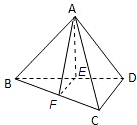 解:(Ⅰ)∵直二面角A-BD-C是由一付直角三角板拼成
解:(Ⅰ)∵直二面角A-BD-C是由一付直角三角板拼成
又∵AB=AD=2,则△ABD是以A为直角的等腰直角三角形,BD=2
又∵∠BCD=90°,∠BDC=60°,
∴CD=
,BC=
,S△BCD=
•
•
=
取BD的中点E,连接AE,则AE⊥BD,AE=
,如图所示
则AE⊥平面BCD,
则VA-BCD=
•AE•S△BCD=
•
•
=
(Ⅱ)过E点做EF∥CD,则EF=
,且EF⊥BC
又∵AE⊥BC,AE∩EF=E
则BC⊥平面AEF
∴AF⊥BC,则线段AF长即为A点到BC的距离
在直角三角形AEF中,AF=
=
=
=
 解:(Ⅰ)∵直二面角A-BD-C是由一付直角三角板拼成
解:(Ⅰ)∵直二面角A-BD-C是由一付直角三角板拼成又∵AB=AD=2,则△ABD是以A为直角的等腰直角三角形,BD=2
| 2 |
又∵∠BCD=90°,∠BDC=60°,
∴CD=
| 2 |
| 6 |
| 1 |
| 2 |
| 2 |
| 6 |
| 3 |
取BD的中点E,连接AE,则AE⊥BD,AE=
| 2 |
则AE⊥平面BCD,
则VA-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
(Ⅱ)过E点做EF∥CD,则EF=
| ||
| 2 |
又∵AE⊥BC,AE∩EF=E
则BC⊥平面AEF
∴AF⊥BC,则线段AF长即为A点到BC的距离
在直角三角形AEF中,AF=
| AE2+EF2 |
2+
|
|
| ||
| 2 |
点评:本题考查的知识点是空间点、线、面的距离计算,棱锥的体积,其判断AE⊥平面BCD(即AE是平面BCD上的高)及判断AF垂直BC(即AF长为点A到BC的距离)是解答本题的关键.

练习册系列答案
相关题目
 如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,
如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°, 如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,
如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,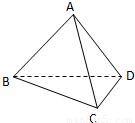 如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,
如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,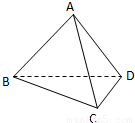 如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,
如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,