题目内容
已知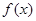 是
是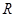 上的偶函数,若将
上的偶函数,若将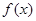 的图象向右平移一个单位后,则得到一个奇函数的图象, 若
的图象向右平移一个单位后,则得到一个奇函数的图象, 若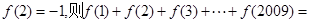 ( )
( )
A. | B.1 | C.-1 | D.-1004.5 |
A
解析考点:偶函数;奇函数;函数的值.
专题:计算题.
分析:法一:由题意f(x)是R上的偶函数,f(x-1)是R上的奇函数,由此可以得出函数的周期为4,再由f(2)=-1求出f(-2)=-1,由奇函数的性质得出f(-1)=0,从而可得f(1)=0,求出一个周期上的四个函数的和,即可求出f(1)+f(2)+f(3)+…+f(2009)的值.
法二:
解答:解:法一:由题意f(x)是R上的偶函数,f(x-1)是R上的奇函数,
f(-x)=f(x),f(-x-1)=-f(x-1),①
∴f(-x-1)=f(x+1),②
由①②得f(x+1)=-f(x-1)③恒成立,
∴f(x-1)=-f(x-3)④
由③④得f(x+1)=f(x-3)恒成立,
∴函数的周期是4,下研究函数一个周期上的函数的值
由于f(x)的图象向右平移一个单位后,则得到一个奇函数的图象即f(0-1)=0,即f(-1)=0,由偶函数知f(1)=0,由周期性知f(3)=0
由f(2)=-1得f(-2)=-1,由f(x+1)=-f(x-1),知f(0)=1,故f(4)=1
故有f(1)+f(2)+f(3)+f(4)=0
∴f(1)+f(2)+f(3)+…+f(2009)=f(2009)=f(1)="0"
故选A
点评:本题考查函数奇偶性的运用,求解本题的关键是根据函数的性质求出函数的周期以及一个周期中函数值的和,然后根据周期性求出函数值的和.

 阅读快车系列答案
阅读快车系列答案下列函数中,在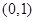 为单调递减的偶函数是
为单调递减的偶函数是
A.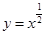 | B.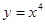 | C.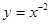 | D.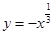 |
函数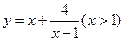 的最小值是 ( )
的最小值是 ( )
| A. 4 | B.5 | C.6 | D.7 |
函数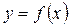 定义在
定义在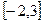 上,则函数
上,则函数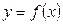 图象与直
图象与直 线
线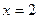 的交点个数有( )
的交点个数有( )
| A.0个 | B.1个 | C.2个 | D.不能确定 |
函数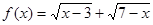 的定义域是( )
的定义域是( )
A.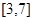 | B.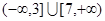 | C.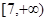 | D.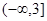 |
函数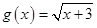 的定义域为( )
的定义域为( )
A.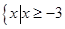 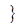 | B.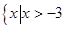 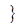 | C. 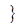 | D.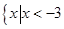 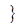 |
设函数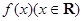 为奇函数,
为奇函数,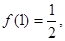
 = ( )
= ( )
| A.0 | B.1 |
C.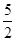 | D.5 |
设函数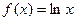 ,当
,当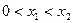 下列结论正确的是( )
下列结论正确的是( )
A. 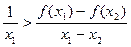 | B. |
C.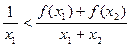 | D.以上都不对。 |
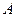 是单位圆上的一定点,动点
是单位圆上的一定点,动点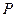 从点
从点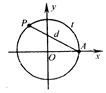
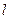 ,弦
,弦 的长为
的长为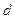 ,则函数
,则函数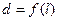 的图像大致是
的图像大致是