题目内容
若将函数y=tan(ωx+
)(ω>0)的图象向右平移
个单位长度后,与函数y=tan(ωx+
)的图象重合,则ω的最小值为( )
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据图象的平移求出平移后的函数解析式,与函数y=tan(ωx+
)的图象重合,比较系数,求出ω=6k+
(k∈Z),然后求出ω的最小值.
| π |
| 6 |
| 1 |
| 2 |
解答:解:y=tan(ωx+
),向右平移
个单位可得:y=tan[ω(x-
)+
]=tan(ωx+
)
∴
-
ω+kπ=
∴ω=6k+
(k∈Z),
又∵ω>0
∴ωmin=
.
故选D.
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
∴
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
∴ω=6k+
| 1 |
| 2 |
又∵ω>0
∴ωmin=
| 1 |
| 2 |
故选D.
点评:本题是基础题,考查三角函数的图象的平移,待定系数法的应用,考查计算能力,是常考题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
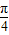 )(ω>0)的图象向右平移
)(ω>0)的图象向右平移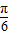 个单位长度后,与函数y=tan(ωx+
个单位长度后,与函数y=tan(ωx+ )的图象重合,则ω的最小值为( )
)的图象重合,则ω的最小值为( )



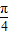 )(ω>0)的图象向右平移
)(ω>0)的图象向右平移 个单位长度后,与函数y=tan(ωx+
个单位长度后,与函数y=tan(ωx+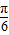 )的图象重合,则ω的最小值为( )
)的图象重合,则ω的最小值为( )


