题目内容
已知函数 ,
, .
.(I)设x=x是函数y=f(x)图象的一条对称轴,求g(x)的值;
(II)求函数h(x)=f(x)+g(x)的单调递增区间.
【答案】分析:(1)先对函数f(x)根据二倍角公式进行化简,再由x=x是函数y=f(x)图象的一条对称轴求出x的值后代入到函数g(x)中,对k分奇偶数进行讨论求值.
(2)将函数f(x)、g(x)的解析式代入到h(x)中化简整理成y=Asin(wx+ρ)+b的形式,得到h(x)=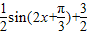 ,然后令
,然后令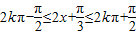 求出x的范围即可.
求出x的范围即可.
解答:解:(I)由题设知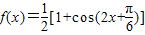 .
.
因为x=x是函数y=f(x)图象的一条对称轴,所以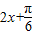 =kπ,
=kπ,
即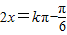 (k∈Z).
(k∈Z).
所以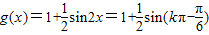 .
.
当k为偶数时,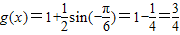 ,
,
当k为奇数时,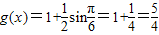 .
.
(II)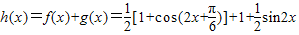
=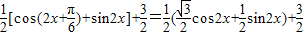
=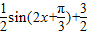 .
.
当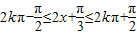 ,即
,即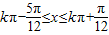 (k∈Z)时,
(k∈Z)时,
函数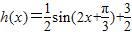 是增函数,
是增函数,
故函数h(x)的单调递增区间是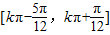 (k∈Z).
(k∈Z).
点评:本题主要考查三角函数的基本性质--单调性、对称性.考查二倍角公式的运用.
(2)将函数f(x)、g(x)的解析式代入到h(x)中化简整理成y=Asin(wx+ρ)+b的形式,得到h(x)=
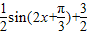 ,然后令
,然后令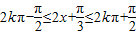 求出x的范围即可.
求出x的范围即可.解答:解:(I)由题设知
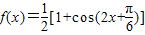 .
.因为x=x是函数y=f(x)图象的一条对称轴,所以
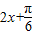 =kπ,
=kπ,即
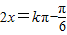 (k∈Z).
(k∈Z).所以
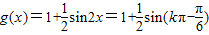 .
.当k为偶数时,
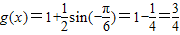 ,
,当k为奇数时,
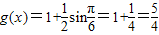 .
.(II)
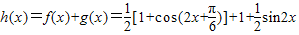
=
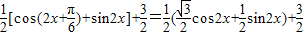
=
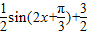 .
.当
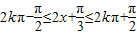 ,即
,即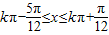 (k∈Z)时,
(k∈Z)时,函数
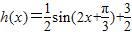 是增函数,
是增函数,故函数h(x)的单调递增区间是
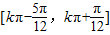 (k∈Z).
(k∈Z).点评:本题主要考查三角函数的基本性质--单调性、对称性.考查二倍角公式的运用.

练习册系列答案
相关题目
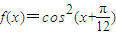 ,
,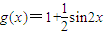 .
.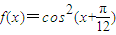 ,
,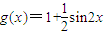 .
.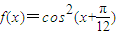 ,
,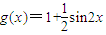 .
. ,
,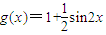 .
.