题目内容
(2012•东城区二模)已知点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,给出下列说法:
①3a-4b+10>0;
②当a>0时,a+b有最小值,无最大值;
③
>2;
④当a>0且a≠1,b>0时,
的取值范围为(-∞,-
)∪(
,+∞).
其中,所有正确说法的序号是
①3a-4b+10>0;
②当a>0时,a+b有最小值,无最大值;
③
| a2+b2 |
④当a>0且a≠1,b>0时,
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
其中,所有正确说法的序号是
③④
③④
.分析:根据点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,我们可以画出点A(a,b)所在的平面区域,进而结合二元一次不等式的几何意义,两点之间距离公式的几何意义,及两点之间连线斜率的几何意义,逐一分析四个答案.可得结论.
解答:解:∵点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,
故点A(a,b)在如图所示的平面区域内
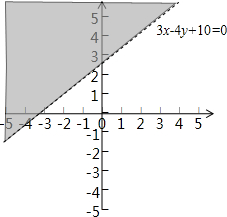
故3a-4b+10<0,即①错误;
当a>0时,a+b>
,a+b即无最小值,也无最大值,故②错误;
设原点到直线3x-4y+10=0的距离为d,则d=
=2,则
>d=2,故③正确;
当a>0且a≠1,b>0时,
表示点A(a,b)与B(1,0)连线的斜率
∵当a=0,b=
时,
=-
,又∵直线3x-4y+10=0的斜率为
故
的取值范围为(-∞,-
)∪(
,+∞),故④正确;
故答案为:③④
故点A(a,b)在如图所示的平面区域内

故3a-4b+10<0,即①错误;
当a>0时,a+b>
| 5 |
| 2 |
设原点到直线3x-4y+10=0的距离为d,则d=
| 10 | ||
|
| a2+b2 |
当a>0且a≠1,b>0时,
| b |
| a-1 |
∵当a=0,b=
| 5 |
| 2 |
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
故
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
故答案为:③④
点评:本题考查的知识点是命题的真假判断与应用,线性规划的简单应用,熟练掌握相关的几个几何意义是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目