题目内容
已知直线y=-2与函数y=tan(ωx+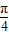 )图象相邻两交点间的距离为
)图象相邻两交点间的距离为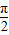 ,将y=tan(ωx+
,将y=tan(ωx+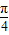 )图象向右平移φ(φ>0)个单位后,其图象关于原点对称,则φ的最小值为( )
)图象向右平移φ(φ>0)个单位后,其图象关于原点对称,则φ的最小值为( )A.
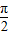
B.
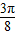
C.
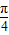
D.
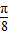
【答案】分析:由题意求出函数的周期,确定ω,利用平移后函数的对称性求出φ的最小值即可.
解答:解:因为直线y=-2与函数y=tan(ωx+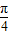 )图象相邻两交点间的距离为
)图象相邻两交点间的距离为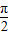 ,
,
所以T=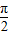 ,所以
,所以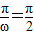 ,ω=2,
,ω=2,
将y=tan(2x+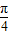 )图象向右平移φ(φ>0)个单位后,
)图象向右平移φ(φ>0)个单位后,
得到函数y=tan[2(x-φ)+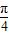 ]=tan(2x-2φ+
]=tan(2x-2φ+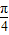 ),
),
其图象关于原点对称,所以φ的最小值为2φ=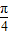 ,所以φ=
,所以φ=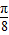 ,
,
故选D.
点评:本题考查三角函数的解析式的求法,三角函数的图象的平移,考查计算能力.
解答:解:因为直线y=-2与函数y=tan(ωx+
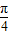 )图象相邻两交点间的距离为
)图象相邻两交点间的距离为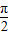 ,
,所以T=
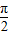 ,所以
,所以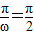 ,ω=2,
,ω=2,将y=tan(2x+
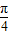 )图象向右平移φ(φ>0)个单位后,
)图象向右平移φ(φ>0)个单位后,得到函数y=tan[2(x-φ)+
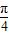 ]=tan(2x-2φ+
]=tan(2x-2φ+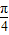 ),
),其图象关于原点对称,所以φ的最小值为2φ=
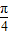 ,所以φ=
,所以φ=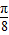 ,
,故选D.
点评:本题考查三角函数的解析式的求法,三角函数的图象的平移,考查计算能力.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知函教f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与直线y=b(0<b<A)的三个相邻交点的横坐标分别是2,4,8,则f(x)的单调递增区间是( )
| A、[6kπ,6kπ+3],k∈Z | B、[6k-3,6k],k∈Z | C、[6k,6k+3],k∈Z | D、[6kπ-3,6kπ],k∈Z |
 的图象与直线y = b (0<b<A)的三个相邻交点的横坐标分别是2,4,8,则
的图象与直线y = b (0<b<A)的三个相邻交点的横坐标分别是2,4,8,则 的单调递增区间是( )
的单调递增区间是( ) B.
B. 
 D.
无法确定
D.
无法确定