题目内容
已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则<a,b>= .
【答案】分析:利用两个向量垂直,数量积等于0,可得  •
•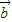 =
= |
|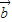 |2,进而可得|
|2,进而可得|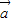 |=|
|=|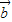 |,代入两个向量的夹角公式可得cos<
|,代入两个向量的夹角公式可得cos<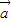 ,
,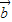 >=
>= ,即可得答案.
,即可得答案.
解答:解:由条件知(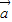 +3
+3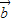 •(7
•(7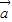 -5
-5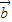 )=7|
)=7|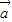 |2-15|
|2-15|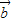 |2+16
|2+16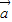 •
•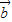 =0,
=0,
及( -4
-4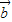 )•(7
)•(7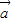 -2
-2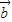 )=7|
)=7|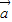 2+8|
2+8|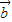 |2-30
|2-30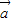 •
•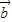 =0.两式相减得46
=0.两式相减得46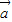 •
•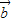 =23|
=23|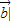 2,
2,
∴ •
•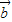 =
= |
|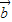 |2.代入上面两个式子中的任意一个,即可得到|
|2.代入上面两个式子中的任意一个,即可得到|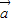 |=|
|=|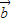 |.
|.
∴cos<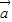 ,
,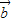 >=
>=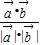 =
=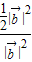 =
= ,∴<
,∴<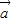 ,
,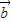 >=60°,
>=60°,
故答案为 60°.
点评:本题考查两个向量垂直的性质,两个向量的数量积的运算,两个向量的夹角公式的应用.
 •
•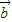 =
= |
|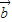 |2,进而可得|
|2,进而可得|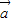 |=|
|=|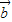 |,代入两个向量的夹角公式可得cos<
|,代入两个向量的夹角公式可得cos<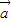 ,
,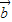 >=
>= ,即可得答案.
,即可得答案.解答:解:由条件知(
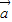 +3
+3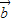 •(7
•(7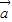 -5
-5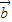 )=7|
)=7|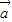 |2-15|
|2-15|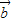 |2+16
|2+16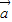 •
•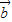 =0,
=0,及(
 -4
-4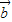 )•(7
)•(7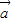 -2
-2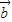 )=7|
)=7|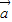 2+8|
2+8|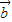 |2-30
|2-30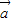 •
•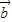 =0.两式相减得46
=0.两式相减得46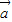 •
•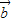 =23|
=23|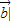 2,
2,∴
 •
•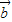 =
= |
|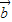 |2.代入上面两个式子中的任意一个,即可得到|
|2.代入上面两个式子中的任意一个,即可得到|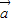 |=|
|=|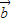 |.
|.∴cos<
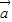 ,
,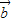 >=
>=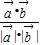 =
=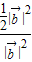 =
= ,∴<
,∴<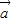 ,
,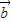 >=60°,
>=60°,故答案为 60°.
点评:本题考查两个向量垂直的性质,两个向量的数量积的运算,两个向量的夹角公式的应用.

练习册系列答案
相关题目