题目内容
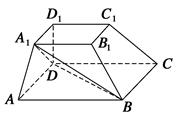
如图, 平面
平面 ,
, 是矩形,
是矩形, ,点
,点 是
是 的中点,点
的中点,点 是边
是边 上的动点.
上的动点.
(Ⅰ)求三棱锥 的体积;
的体积;
(Ⅱ)当点 为
为 的中点时,试判断
的中点时,试判断 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅲ)证明:无论点 在边
在边 的何处,都有
的何处,都有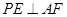 .
.
(Ⅰ)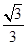 ;(Ⅱ)
;(Ⅱ) 与
与 平面平行;(Ⅲ)证明见解析.
平面平行;(Ⅲ)证明见解析.
解析试题分析:﹙Ⅰ﹚将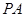 为高,
为高,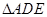 为底面可根据条件直接求得体积;(Ⅱ)根据三角形的中位线的性质及线面平行的判定性质易判断
为底面可根据条件直接求得体积;(Ⅱ)根据三角形的中位线的性质及线面平行的判定性质易判断 为
为 的中点时,有
的中点时,有 与
与 平面平行;(Ⅲ)根据条件只须证明
平面平行;(Ⅲ)根据条件只须证明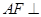 平面
平面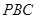 ,进而转化为证明
,进而转化为证明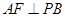 与
与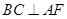 即可,
即可,
试题解析:(Ⅰ)解:∵ ⊥平面
⊥平面 ,
, 为矩形,
为矩形,
∴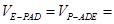
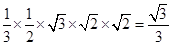 .
.
(Ⅱ) 与
与 平面平行.
平面平行.
当 为
为 中点时,
中点时, 为
为 的中点,∴
的中点,∴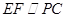 ,
,
∵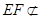 平面
平面 ,
,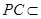 平面
平面 ,∴
,∴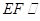 平面
平面 .
.
(Ⅲ)证明:∵ ,
, 为
为 的中点,∴
的中点,∴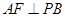 ,
,
∵ 平面
平面 ,∴
,∴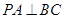 ,
,
又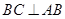 ,∴
,∴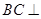 平面
平面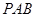 ,
,
又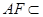 平面
平面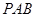 ,∴
,∴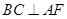 ,
,
又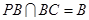 ,∴
,∴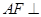 平面
平面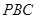 ,
,
因无论点 在边
在边 的何处,都有
的何处,都有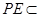 平面
平面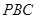 ,∴
,∴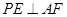 .
.
考点:1、线面垂直;2、线面平行;3、线线垂直.

练习册系列答案
相关题目
 中,点
中,点 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且 ,
,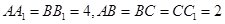 ,E为
,E为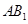 中点,
中点,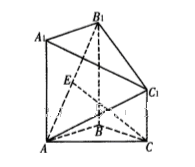
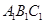 ,
,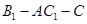 的大小.
的大小. 中,
中, 分别为
分别为 的中点.
的中点.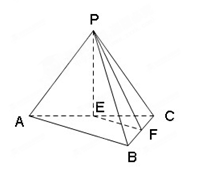
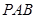 ;
;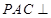 平面
平面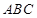 ,且
,且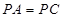 ,
,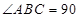 º,求证:平面
º,求证:平面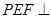 平面
平面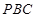
 .
.
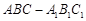 中,
中,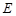 ,
,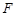 分别为
分别为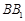 ,
,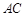 的中点.
的中点.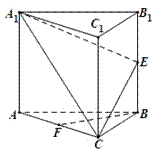
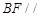 平面
平面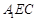 ;
;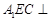 平面
平面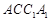 .
. 所在平面与正
所在平面与正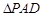 所在平面互相垂直,
所在平面互相垂直,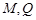 分别为
分别为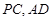 的中点.
的中点.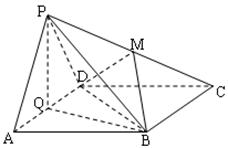
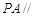 平面
平面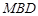 ;
;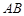 上是否存在一点
上是否存在一点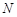 ,使得平面
,使得平面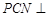 平面
平面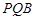 ?若存在,试指出点
?若存在,试指出点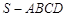 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面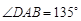 ,
,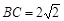 ,
,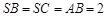 ,
, 为线段
为线段 的中点.
的中点.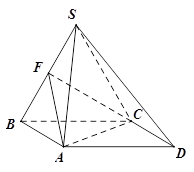
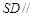 平面
平面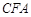 ;
; 与面
与面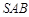 所成二面角大小.
所成二面角大小. ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.