Question

已知两直线a₁x+b₁y+1=0和a₂x+b₂y+1=0的交点为P(2,3),求过两点A(a₁,b₁)、B(a₂,b₂)的直线方程.

Answer 1

解法一:因为P(2,3)是两直线的交点,

所以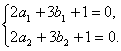

两式相减得2(a₁-a₂)+3(b₁-b₂)=0,

即.

故所求直线方程为y-b₁=(x-a₁).

所以2x+3y-(2a₁+3b₁)=0.

又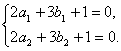

故过两点A(a₁,b₁)、B(a₂,b₂)的直线方程为2x+3y+1=0.

解法二:因为P(2,3)是两直线的交点,

所以2a₁+3b₁+1=0,2a₂+3b₂+1=0.

可见A(a₁,b₁)、B(a₂,b₂)都满足方程2x+3y+1=0.

故过两点A(a₁,b₁)、B(a₂,b₂)的直线方程为2x+3y+1=0.