题目内容
 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象.
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象.(1)求函数解析式;
(2)当x∈R时,求该函数图象的对称轴方程和对称中心坐标;
(3)当x∈R时,写出f(x)的单调增区间;
(4)当x∈R时,求使f(x)≥1 成立的x 的取值集合;
(5)当x∈[
| π |
| 12 |
| π |
| 2 |
分析:(1)由图可得A=2,由T=π可求得ω=2,由又
=
可求得φ;
(2)由2x+
=kπ+
可求其对称轴方程,由2x+
=kπ可求其对称中心坐标;
(3)由2kπ-
≤2x+
≤2kπ+
,k∈Z可得f(x)的单调增区间;
(4)由2kπ+
≤2x+
≤2kπ+
,k∈Z,可求使f(x)≥1 成立的x 的取值集合;
(5)x∈[
,
],2x+
∈[
,
],从而可求求f(x)的值域.
| ||
| ω |
| π |
| 6 |
(2)由2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
(3)由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(4)由2kπ+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
(5)x∈[
| π |
| 12 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 7π |
| 6 |
解答:解:(1)由图象可得:A=2,(1分)
T=2(
-
)=π=
,
∴ω=2(3分)
又
=
,
∴φ=
(5分)
所以f(x)=2sin(2x+
)(6分)
(2)由2x+
=kπ+
,k∈Z得其对称轴方程为:x=
+
,k∈Z;对称中心坐标为:(
-
,);
(3)由2kπ-
≤2x+
≤2kπ+
,k∈Z得:(8分)
kπ-
≤x≤kπ+
,k∈Z(9分)
所以f(x)的增区间是[kπ-
,kπ+
],(k∈Z)(10分)
(4)由f(x)≥1得2sin(2x+
)≥1,
∴sin(2x+
)≥
,
所以,2kπ+
≤2x+
≤2kπ+
,k∈Z,
解得:kπ≤x≤kπ+
,k∈Z,
∴f(x)≥1 成立的x 的取值集合为{x|kπ≤x≤kπ+
,k∈Z}(12分)
(5)∵x∈[
,
],
∴2x+
∈[
,
].
当2x+
=
,即x=
时,f(x)取得最大值2;
当2x+
=
,即x=
时,f(x)取得最小值-1,故f(x)的值域为[-1,2].
T=2(
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| ω |
∴ω=2(3分)
又
| ||
| ω |
| π |
| 6 |
∴φ=
| π |
| 6 |
所以f(x)=2sin(2x+
| π |
| 6 |
(2)由2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
(3)由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
kπ-
| π |
| 3 |
| π |
| 6 |
所以f(x)的增区间是[kπ-
| π |
| 3 |
| π |
| 6 |
(4)由f(x)≥1得2sin(2x+
| π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
所以,2kπ+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
解得:kπ≤x≤kπ+
| π |
| 3 |
∴f(x)≥1 成立的x 的取值集合为{x|kπ≤x≤kπ+
| π |
| 3 |
(5)∵x∈[
| π |
| 12 |
| π |
| 2 |
∴2x+
| π |
| 6 |
| π |
| 3 |
| 7π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
当2x+
| π |
| 6 |
| 7π |
| 6 |
| π |
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性,对称性,定义域与最值,属于三角的综合应用,是难题.

练习册系列答案
相关题目
 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象 ,
, ],求f(x)的值域.
],求f(x)的值域.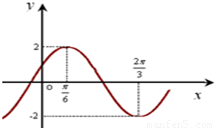
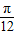 ,
,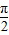 ],求f(x)的值域.
],求f(x)的值域.
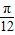 ,
, ],求f(x)的值域.
],求f(x)的值域.