题目内容
已知椭圆C:
 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程;
(2)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的
对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
【答案】
(1) ;(2)定点
;(2)定点 (1,0).
(1,0).
【解析】
试题分析:(1)求椭圆C的方程,由题意,焦点坐标为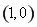 ,可求得
,可求得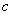 ,再根据椭圆两个焦点与短轴的一个端点构成等边三角形.由等边三角形的性质,可求得
,再根据椭圆两个焦点与短轴的一个端点构成等边三角形.由等边三角形的性质,可求得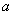 和
和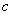 的关系式,可求得
的关系式,可求得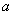 ,进而求得
,进而求得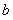 ,则椭圆的方程可得;(2)求证:直线
,则椭圆的方程可得;(2)求证:直线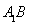 过
过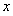 轴上一定点,并求出此定点坐标.这是过定点问题,这类题的处理方法有两种,一.可设出直线方程为
轴上一定点,并求出此定点坐标.这是过定点问题,这类题的处理方法有两种,一.可设出直线方程为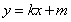 ,然后利用条件建立
,然后利用条件建立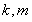 等量关系进行消元,借助于直线系的思想找出定点.二.从特殊情况入手,先探求定点,再证明与变量无关.本题可设直线
等量关系进行消元,借助于直线系的思想找出定点.二.从特殊情况入手,先探求定点,再证明与变量无关.本题可设直线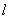 的方程为:
的方程为: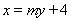 ,与椭圆方程
,与椭圆方程 联立消去
联立消去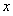 ,设出
,设出 ,
,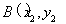 ,则可利用韦达定理求得
,则可利用韦达定理求得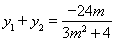 和
和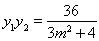 的表达式,根据
的表达式,根据 点坐标求得关于
点坐标求得关于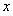 轴对称的点
轴对称的点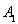 的坐标,设出定点
的坐标,设出定点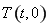 ,利用
,利用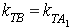 求得
求得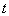 ,从而得证.
,从而得证.
试题解析:(1)椭圆C: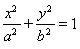
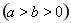 的一个焦点是(1,0),所以半焦距
的一个焦点是(1,0),所以半焦距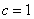 ,又因为椭圆两个焦点与短轴的一个端点构成等边三角形,所以
,又因为椭圆两个焦点与短轴的一个端点构成等边三角形,所以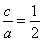 ,解得
,解得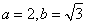 ,所以椭圆C的标准方程为
,所以椭圆C的标准方程为 ;· 5分
;· 5分
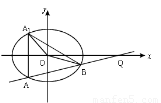
(2)设直线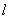 :
: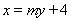 与
与 联立并消去
联立并消去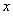 得:
得:
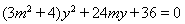 .
.
记 ,
,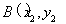 ,
,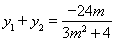 ,
,
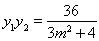 . 8分
. 8分
由A关于 轴的对称点为
轴的对称点为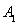 ,得
,得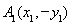 ,根据题设条件设定点为
,根据题设条件设定点为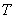 (
(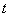 ,0),
,0),
得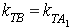 ,即
,即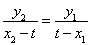 .
.
所以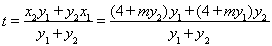
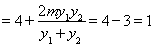
即定点 (1,0). 13分
(1,0). 13分
考点:椭圆的简单性质;椭圆的标准方程;直线与圆锥曲线的综合问题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
 的离心率e=
的离心率e= ,左右两个焦分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=2.
,左右两个焦分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=2.