题目内容
a、b是常数,关于x的一元二次方程x2+(a+b)x+3+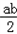 =0有实数解记为事件A.
=0有实数解记为事件A.
(1)若a、b分别表示投掷两枚均匀骰子出现的点数,求P(A);
(2)若a∈R、b∈R,﹣6≤a+b≤6且﹣6≤a﹣b≤6,求P(A).
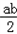 =0有实数解记为事件A.
=0有实数解记为事件A.(1)若a、b分别表示投掷两枚均匀骰子出现的点数,求P(A);
(2)若a∈R、b∈R,﹣6≤a+b≤6且﹣6≤a﹣b≤6,求P(A).
解:(1)方程有实数解,(a+b)2﹣4(3+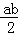 )≥0,即a2+b2≥12
)≥0,即a2+b2≥12
依题意,a=1、2、3、4、5、6,b=1、2、3、4、5、6,
所以,“投掷两枚均匀骰子出现的点数”共有6×6=36种结果
当且仅当“a=1且b=1、2、3”,或“a=2且b=1、2”,或“a=3且b=1”时,a2+b2≥12不成立,
所以满足a2+b2≥12的结果有36﹣(3+2+1)=30种,
从而P(A)=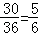 .
.
(2)在平面直角坐标系aOb中,直线a+b=±6与a﹣b=±6 围成一个正方形
正方形边长即直线a+b=±6与a﹣b=±6之间的距离为d=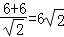
正方形的面积S=d2=72,
圆a2+b2=12的面积为S′=12π,圆在正方形内部,
所以P(A)=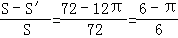 .
.
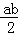 )≥0,即a2+b2≥12
)≥0,即a2+b2≥12依题意,a=1、2、3、4、5、6,b=1、2、3、4、5、6,
所以,“投掷两枚均匀骰子出现的点数”共有6×6=36种结果
当且仅当“a=1且b=1、2、3”,或“a=2且b=1、2”,或“a=3且b=1”时,a2+b2≥12不成立,
所以满足a2+b2≥12的结果有36﹣(3+2+1)=30种,
从而P(A)=
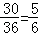 .
.(2)在平面直角坐标系aOb中,直线a+b=±6与a﹣b=±6 围成一个正方形
正方形边长即直线a+b=±6与a﹣b=±6之间的距离为d=
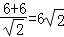
正方形的面积S=d2=72,
圆a2+b2=12的面积为S′=12π,圆在正方形内部,
所以P(A)=
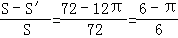 .
. 
练习册系列答案
相关题目
 =0有实数解记为事件A.
=0有实数解记为事件A.