Ő‚ńŅńŕ»›
“—÷™Sn=a1Cn1+a2Cn2+a3Cn3+a4Cn4+°≠+anCnn£¨bn=n•2n
£®1£©»Ű{an} «Ķ»≤Ó żŃ–£¨«“ ◊ŌÓ «(
-
)6’ĻŅ™ ĹĶń≥£ żŌÓĶń
£¨Ļę≤Ódő™(
-
)6’ĻŅ™ ĹĶńłųŌÓŌĶ żļÕĘŔ«ůS2£¨S3£¨S4£¨Ęŕ’“≥ŲSn”ŽbnĶńĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£ģ
£®2£©»Űan=
(q°Ŕ°ņ1)£¨«“ żŃ–{cn}¬ķ◊„c1+c2+c3+°≠+cn=
£¨«ů÷§£ļ{cn} «Ķ»Ī» żŃ–£ģ
£®1£©»Ű{an} «Ķ»≤Ó żŃ–£¨«“ ◊ŌÓ «(
| x |
| 2 |
| x |
| 1 |
| 60 |
| x |
| 2 |
| x |
£®2£©»Űan=
| qn-1 |
| q-1 |
| Sn |
| 2n |
∑÷őŲ£ļ£®1£©ņŻ”√∂ĢŌÓ Ĺ∂®ņŪ«ů≥Ų£¨a1=1£¨d=1£¨ĘŔņŻ”√◊ťļŌ żĻę ĹŅ…«ů≥ŲS2£¨S3£¨S4£¨ĘŕŅ…Ķ√≥ŲSn=
bn£¨‘Ŕ”√ĶĻ–ÚŌŗľ”∑®÷§√ų£ģ
£®2£©Õ®ŌÓakCnk=
=
qk
-
(q°Ŕ°ņ1)£¨ņŻ”√∑÷◊ť∑®£¨ĹŠļŌ∂ĢŌÓ Ĺ∂®ņŪĶńńś”√°Ę∂ĢŌÓ ĹŌĶ żĶń–‘÷ £¨«ů≥Ų Tn=c1+c2+c3+°≠+cn=
=
[(
)n-1]£ģ‘ŔņŻ”√ żŃ–Tn”ŽcnĶńĻōŌĶ«ů≥Ųcn=
(
)n-1£¨ī”∂Ý“◊÷§{cn} «Ķ»Ī» żŃ–£ģ
| 1 |
| 2 |
£®2£©Õ®ŌÓakCnk=
| qk-1 |
| q-1 |
| C | k n |
| 1 |
| q-1 |
| C | k n |
| 1 |
| q-1 |
| C | k n |
| Sn |
| 2n |
| 1 |
| q-1 |
| 1+q |
| 2 |
| 1 |
| 2 |
| 1+q |
| 2 |
Ĺ‚īū£ļĹ‚£ļ£®1£©(
-
)6’ĻŅ™ ĹĶńÕ®ŌÓő™
(
)6-r(-
)r=(-2)r
x3-
r£¨ŃÓ3-
r=0£¨r=2£¨
≥£ żŌÓő™£®-2£©2C62=60£¨a1=1£¨‘ŕ(
-
)6’ĻŅ™ Ĺ÷–ŃÓx=1£¨Ķ√≥ŲłųŌÓŌĶ żļÕő™£®1-2£©6=1£¨ľīd=1£ģan=n£ģ
ĘŔS2=C21+2C22=4£¨S3=C31+2C32+3C33=12£¨S4=C41+2C42+3C43+4C44=32
ĘŕSn=
bn
°ŖSn=Cn1+2Cn2+3Cn3+4Cn4+°≠+nCnn
”÷ Sn=nCnn+£®n-1£©Cn n-1+£®n-2£©Cn n-2+£®n-3£©Cn n-3+°≠+Cn1
ŃĹ ĹŌŗľ”Ķ√2Sn=Cn1+n£®Cn1+Cn2+Cn3+Cn4+°≠+Cnn-1£©+nCnn=n£®2n-Cn0-Cnn£©+2n=n•2n=b n
°ŗSn=
bn£ģ
£®2£©°ŖakCnk=
=
qk
-
(q°Ŕ°ņ1)
°ŗSn=
qk
-
=
[(1+q)n-1 ]-
£®2n-1£©=
[£®1+q£©n-2n]£ģ
°ŗTn=c1+c2+c3+°≠+cn=
=
[(
)n-1]£ģ
ĶĪn=1 Ī£¨c1=T1=
=
£ģ
ĶĪn°›2 Ī cn=Tn-Tn-1=
[(
)n-(
)n-1]=
(
)n-1£¨∂‘n=1 Ī“≤≥…ŃĘ£ģ
°ŗcn=
(
)n-1£¨{cn} «“‘
ő™ ◊ŌÓ£¨“‘(
) ő™ĻęĪ»ĶńĶ»Ī» żŃ–£ģ
| x |
| 2 |
| x |
| C | r 6 |
| x |
| 2 |
| x |
| C | r 6 |
| 3 |
| 2 |
| 3 |
| 2 |
≥£ żŌÓő™£®-2£©2C62=60£¨a1=1£¨‘ŕ(
| x |
| 2 |
| x |
ĘŔS2=C21+2C22=4£¨S3=C31+2C32+3C33=12£¨S4=C41+2C42+3C43+4C44=32
ĘŕSn=
| 1 |
| 2 |
°ŖSn=Cn1+2Cn2+3Cn3+4Cn4+°≠+nCnn
”÷ Sn=nCnn+£®n-1£©Cn n-1+£®n-2£©Cn n-2+£®n-3£©Cn n-3+°≠+Cn1
ŃĹ ĹŌŗľ”Ķ√2Sn=Cn1+n£®Cn1+Cn2+Cn3+Cn4+°≠+Cnn-1£©+nCnn=n£®2n-Cn0-Cnn£©+2n=n•2n=b n
°ŗSn=
| 1 |
| 2 |
£®2£©°ŖakCnk=
| qk-1 |
| q-1 |
| C | k n |
| 1 |
| q-1 |
| C | k n |
| 1 |
| q-1 |
| C | k n |
°ŗSn=
| 1 |
| q-1 |
| n |
 |
| k=1 |
| C | k n |
| 1 |
| q-1 |
| n |
 |
| k=1 |
| C | k n |
| 1 |
| q-1 |
| 1 |
| q-1 |
| 1 |
| q-1 |
°ŗTn=c1+c2+c3+°≠+cn=
| Sn |
| 2n |
| 1 |
| q-1 |
| 1+q |
| 2 |
ĶĪn=1 Ī£¨c1=T1=
| 1 |
| q-1 |
| q-1 |
| 2 |
| 1 |
| 2 |
ĶĪn°›2 Ī cn=Tn-Tn-1=
| 1 |
| q-1 |
| 1+q |
| 2 |
| 1+q |
| 2 |
| 1 |
| 2 |
| 1+q |
| 2 |
°ŗcn=
| 1 |
| 2 |
| 1+q |
| 2 |
| 1 |
| 2 |
| 1+q |
| 2 |
Ķ„∆ņ£ļ÷ōĶ„Ņľ≤ž∂ĢŌÓ Ĺ∂®ņŪĶń”¶”√£¨Ĺ‚ĺŲĶń∑Ĺ∑®”–ĶĻ–ÚŌŗľ”∑®«ůļÕ£¨ņŻ”√ żŃ–ļÕĶń∂®“Ś«ůÕ®ŌÓ£¨ń—Ķ„‘ŕ”ŕ◊ŘļŌ∑÷őŲ£¨Ňšī’ńś”√∂ĢŌÓ Ĺ∂®ņŪ£¨ Ű”ŕń—Ő‚£ģŅľ≤ťľ∆ň„°ĘĽĮľÚń‹Ń¶£ģ

Ń∑Ōį≤ŠŌĶŃ–īūįł
ŌŗĻōŐ‚ńŅ
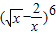 ’ĻŅ™ ĹĶń≥£ żŌÓĶń
’ĻŅ™ ĹĶń≥£ żŌÓĶń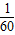 £¨Ļę≤Ódő™
£¨Ļę≤Ódő™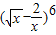 ’ĻŅ™ ĹĶńłųŌÓŌĶ żļÕĘŔ«ůS2£¨S3£¨S4£¨Ęŕ’“≥ŲSn”ŽbnĶńĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£ģ
’ĻŅ™ ĹĶńłųŌÓŌĶ żļÕĘŔ«ůS2£¨S3£¨S4£¨Ęŕ’“≥ŲSn”ŽbnĶńĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£ģ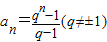 £¨«“ żŃ–{cn}¬ķ◊„
£¨«“ żŃ–{cn}¬ķ◊„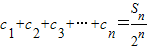 £¨«ů÷§£ļ{cn} «Ķ»Ī» żŃ–£ģ
£¨«ů÷§£ļ{cn} «Ķ»Ī» żŃ–£ģ