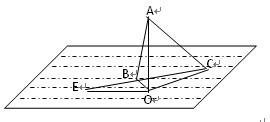
题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解:在Rt△AOB与Rt△AOC中,求得OB= 由余弦定理得BC= 于是船速v=2 分析:解本题需要正确理解题意,选好需要解的三角形. |
(2) |
在△OBC中,由余弦定理得cos∠OBC= 于是sin∠EBO=sin∠OBC= sin∠BEO=sin[ 在△BEO中,由正弦定理得OE= 于是从B到E所需时间t= ∴再经过5分钟到达海岛的正西方向,此时E点离海岛1.5km. |

练习册系列答案
相关题目