题目内容
若m、n都是正整数,那么“m、n中至少有一个等于1”是“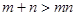 ”的( )
”的( )
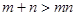 ”的( )
”的( )| A.充分而不必要的条件 | B.必要而不充分的条件 |
| C.充要条件 | D.既不充分也不必要的条件 |
C
析:由m+n>mn,进行移项变形得出(m-1)(n-1)<1,注意这个过程可以逆推,即可得出答案,即前者和后者可以互相推出,得到前者是后者的充要条件.
解答:解:∵m+n>mn,
∴mn-m-n<0,
∵mn-m-n=(m-1)(n-1)-1,
∴(m-1)(n-1)-1<0,
即(m-1)(n-1)<1.
∵m,n是正整数,
∴(m-1)(n-1)=0,
故m和n中至少有一个为1.
上面的过程可以可逆,
故前者是后者的充要条件,
故选:C.
点评:本题考查充分条件、必要条件与充要条件的判断,考查对于至少的理解,本题解题的关键是验证两个条件是否可以互相推出,本题是一个基础题.
解答:解:∵m+n>mn,
∴mn-m-n<0,
∵mn-m-n=(m-1)(n-1)-1,
∴(m-1)(n-1)-1<0,
即(m-1)(n-1)<1.
∵m,n是正整数,
∴(m-1)(n-1)=0,
故m和n中至少有一个为1.
上面的过程可以可逆,
故前者是后者的充要条件,
故选:C.
点评:本题考查充分条件、必要条件与充要条件的判断,考查对于至少的理解,本题解题的关键是验证两个条件是否可以互相推出,本题是一个基础题.

练习册系列答案
相关题目
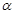 为锐角”是“
为锐角”是“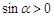 ”成立的 ( )
”成立的 ( ) 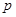 :
: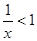 ;条件
;条件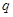 :
: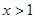 .则
.则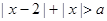 恒成立的一个充分不必要条件是( )
恒成立的一个充分不必要条件是( )



 、
、 为实数,则“
为实数,则“ ”是“
”是“ ”的 ( )
”的 ( )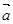 与
与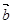 -
-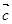 都是非零向量,则“
都是非零向量,则“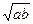 (G≠0)是a,G,b成等比数列的充分非必要条件;②若角α,β满足cosαcosβ=1,则sin(α+β)=0;③若不等式|x-4|+|x-3|<a的解集非空,则必有a≥1;④函数y=sinx+sin|x|的值域是[-2,2].
(G≠0)是a,G,b成等比数列的充分非必要条件;②若角α,β满足cosαcosβ=1,则sin(α+β)=0;③若不等式|x-4|+|x-3|<a的解集非空,则必有a≥1;④函数y=sinx+sin|x|的值域是[-2,2].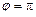 ”是“函数
”是“函数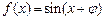 是奇函数”的 ( )
是奇函数”的 ( )