题目内容
已知曲线E:ax2+by2=1(a>0,b>0),经过点M(![]() ,0)的直线l与曲线E交
,0)的直线l与曲线E交
于点A、B,且![]() =-2
=-2![]() .
.
(1)若点B的坐标为(0,2),求曲线E的方程;
(2)若a=b=1,求直线AB的方程.
解:
(1) 设A(x0,y0),因为B(0,2),M(![]() ,0)
,0)
故![]() =(-
=(-![]() ,2),
,2),![]() =(x0-
=(x0-![]() ,y0). ……………………………………2分
,y0). ……………………………………2分
因为![]() =-2
=-2![]() ,所以(-
,所以(-![]() ,2)=-2(x0-
,2)=-2(x0-![]() ,y0).
,y0).
所以x0=![]() ,y0=-1.即A(
,y0=-1.即A(![]() ,-1). ……………………………………4分
,-1). ……………………………………4分
因为A,B都在曲线E上,所以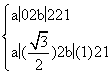 解得a=1,b=
解得a=1,b=![]() .
.
所以曲线E的方程为x2+![]() =1. ……………………………………6分
=1. ……………………………………6分
(2)(法一)当a=b=1时,曲线E为圆:x2+y2=1.设A(x1,y1),B(x2,y2).
因为![]() =-2
=-2![]() ,所以(x2-
,所以(x2-![]() ,y2) =-2(x1-
,y2) =-2(x1-![]() ,y1),即
,y1),即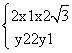
设线段AB的中点为T,则点T的坐标为(![]() ,
,![]() ),即(
),即(![]() ,-
,-![]() ).
).
所以![]() =(
=(![]() ,-
,-![]() ),
),![]() =(x2-x1,y2-y1)=(
=(x2-x1,y2-y1)=(![]() -3x1,-3y1).
-3x1,-3y1).
因为OT⊥AB,所以![]() ×
×![]() =0,即3-4
=0,即3-4![]() x1+3x
x1+3x![]() +3y
+3y![]() =0.
=0.
因为x![]() +y
+y![]() =1,所以x1=
=1,所以x1=![]() ,y1=±
,y1=±![]() .
.
当点A的坐标为(![]() ,-
,-![]() )时,对应的点B的坐标为(0,1),此时直线AB的斜率
)时,对应的点B的坐标为(0,1),此时直线AB的斜率
k=-![]() ,所求直线AB的方程为y=-
,所求直线AB的方程为y=-![]() x+1;
x+1;
当点A的坐标为(![]() ,
,![]() )时,对应的点B的坐标为(0,-1),此时直线AB的斜率k=
)时,对应的点B的坐标为(0,-1),此时直线AB的斜率k=![]() ,
,
所求直线AB的方程为y=![]() x-1. ……………………………………16分
x-1. ……………………………………16分
(法二)当a=b=1时,曲线E为圆:x2+y2=1.设A(x1,y1),B(x2,y2).
因为![]() =-2
=-2![]() ,所以(x2-
,所以(x2-![]() ,y2) =-2(x1-
,y2) =-2(x1-![]() ,y1),即
,y1),即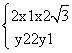
因为点A,B在圆上,所以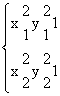
由①×4-②,得(2x1+x2)(2x1-x2)=3.所以2x1-x2=![]() ,解得x1=
,解得x1=![]() ,x2=0.
,x2=0.
 由x1=
由x1=![]() ,得y1=±
,得y1=±![]() .(以下同方法一)
.(以下同方法一)
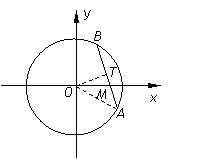
(法三)如图,设AB中点为T.
则TM=TA-MA=![]() AB,OM=
AB,OM=![]() .
.
根据Rt△OTA和Rt△OTM,得
即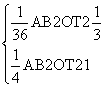 解得AB=
解得AB=![]() ,OT=
,OT=![]() .所以在Rt△OTM中,tanÐOMT=
.所以在Rt△OTM中,tanÐOMT=![]() =
=![]() .
.
所以kAB=-![]() 或
或![]() .所以直线AB的方程为y=-
.所以直线AB的方程为y=-![]() x+1或y=
x+1或y=![]() x-1.
x-1.

 的直线l与曲线E交与点A、B,且
的直线l与曲线E交与点A、B,且 .
. 的直线l与曲线E交与点A、B,且
的直线l与曲线E交与点A、B,且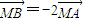 .
.