题目内容
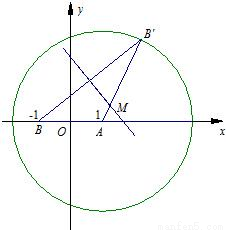
已知点B′为圆A:(x-1)2+y2=8上任意一点、点B(-1,0).线段BB′的垂直平分线和线段AB′相交于点M.(1)求点M的轨迹E的方程;
(2)已知点M(x,y)为曲线E上任意一点.求证:点
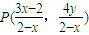 关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.
关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.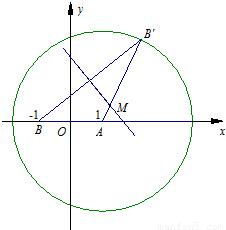
【答案】分析:(1)求出A的坐标,由题意可知M满足椭圆的定义,求a、b可得它的方程.
(2)设出定点利用对称知识,和已知直线垂直,中点在已知直线上,解出定点坐标即可.
解答:解:(1)连接MB,
∴MB=MB',
故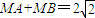 、而AB=2(4分)
、而AB=2(4分)
∴点M的轨迹是以A、B为焦点且长轴长为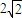 的椭圆.
的椭圆.
∴点M的轨迹E的方程为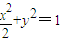 (8分)
(8分)
(2)证明:设点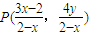
关于直线xx+2yy=2的对称点为Q(a,b)
所以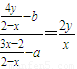 .
.
即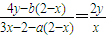 (10分)
(10分)
∴bx(2-x)=2y(2-x)(a+1).
∵x≠2
∴bx-2y(a+1)=0(14分)
因为上式对任意x,y成立,
故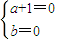
所以对称点为定点Q(-1,0).(16分)
点评:本题考查圆的标准方程,点关于直线对称问题,轨迹的求法,是难题.
(2)设出定点利用对称知识,和已知直线垂直,中点在已知直线上,解出定点坐标即可.
解答:解:(1)连接MB,
∴MB=MB',

故
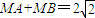 、而AB=2(4分)
、而AB=2(4分)∴点M的轨迹是以A、B为焦点且长轴长为
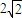 的椭圆.
的椭圆.∴点M的轨迹E的方程为
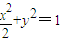 (8分)
(8分)(2)证明:设点
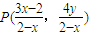
关于直线xx+2yy=2的对称点为Q(a,b)
所以
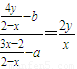 .
.即
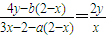 (10分)
(10分)∴bx(2-x)=2y(2-x)(a+1).
∵x≠2
∴bx-2y(a+1)=0(14分)
因为上式对任意x,y成立,
故
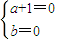
所以对称点为定点Q(-1,0).(16分)
点评:本题考查圆的标准方程,点关于直线对称问题,轨迹的求法,是难题.

练习册系列答案
相关题目
 已知点B′为圆A:(x-1)2+y2=8上任意一点、点B(-1,0).线段BB′的垂直平分线和线段AB′相交于点M.
已知点B′为圆A:(x-1)2+y2=8上任意一点、点B(-1,0).线段BB′的垂直平分线和线段AB′相交于点M.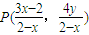 关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.
关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.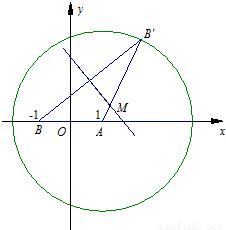
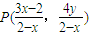 关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.
关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.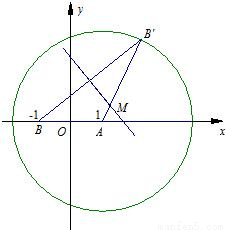
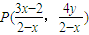 关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.
关于直线xx+2yy=2的对称点为定点、并求出该定点的坐标.