题目内容
函数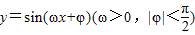 在同一个周期内,当
在同一个周期内,当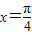 时y取最大值1,当
时y取最大值1,当 时,y取最小值-1.
时,y取最小值-1.(1)求函数的解析式y=f(x).
(2)函数y=sinx的图象经过怎样的变换可得到y=f(x)的图象?
(3)若函数f(x)满足方程f(x)=a(0<a<1),求在[0,2π]内的所有实数根之和.
【答案】分析:(1)通过同一个周期内,当 时y取最大值1,当
时y取最大值1,当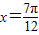 时,y取最小值-1.求出函数的周期,利用最值求出φ,即可求函数的解析式y=f(x).
时,y取最小值-1.求出函数的周期,利用最值求出φ,即可求函数的解析式y=f(x).
(2)函数y=sinx的图象经过左右平移,然后是横坐标变伸缩变换,纵坐标不变,可得到y=f(x)的图象,确定函数解析式.(3)确定函数在[0,2π]内的周期的个数,利用f(x)=a(0<a<1)与函数的对称轴的关系,求出所有实数根之和.
解答:解:(1)∵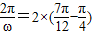 ,
,
∴ω=3,
又因 ,
,
∴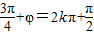 ,又
,又 ,得
,得
∴函数 ;
;
(2)y=sinx的图象向右平移 个单位得
个单位得 的图象,
的图象,
再由 图象上所有点的横坐标变为原来的
图象上所有点的横坐标变为原来的 .纵坐标不变,得到
.纵坐标不变,得到 的图象,
的图象,
(3)∵ 的周期为
的周期为 ,
,
∴ 在[0,2π]内恰有3个周期,
在[0,2π]内恰有3个周期,
∴ 在[0,2π]内有6个实根且
在[0,2π]内有6个实根且
同理, ,
,
故所有实数之和为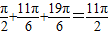 .
.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,正弦函数的图象,考查数形结合的思想,考查计算能力,是中档题.
 时y取最大值1,当
时y取最大值1,当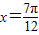 时,y取最小值-1.求出函数的周期,利用最值求出φ,即可求函数的解析式y=f(x).
时,y取最小值-1.求出函数的周期,利用最值求出φ,即可求函数的解析式y=f(x).(2)函数y=sinx的图象经过左右平移,然后是横坐标变伸缩变换,纵坐标不变,可得到y=f(x)的图象,确定函数解析式.(3)确定函数在[0,2π]内的周期的个数,利用f(x)=a(0<a<1)与函数的对称轴的关系,求出所有实数根之和.
解答:解:(1)∵
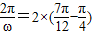 ,
,∴ω=3,
又因
 ,
,∴
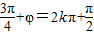 ,又
,又 ,得
,得
∴函数
 ;
;(2)y=sinx的图象向右平移
 个单位得
个单位得 的图象,
的图象,再由
 图象上所有点的横坐标变为原来的
图象上所有点的横坐标变为原来的 .纵坐标不变,得到
.纵坐标不变,得到 的图象,
的图象,(3)∵
 的周期为
的周期为 ,
,∴
 在[0,2π]内恰有3个周期,
在[0,2π]内恰有3个周期,∴
 在[0,2π]内有6个实根且
在[0,2π]内有6个实根且
同理,
 ,
,故所有实数之和为
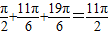 .
.点评:本题考查函数y=Asin(ωx+φ)的图象变换,正弦函数的图象,考查数形结合的思想,考查计算能力,是中档题.

练习册系列答案
相关题目
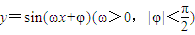 在同一个周期内,当
在同一个周期内,当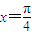 时y取最大值1,当
时y取最大值1,当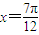 时,y取最小值-1.
时,y取最小值-1.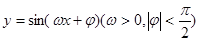 在同一个周期内,当
在同一个周期内,当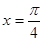 时
时 取最大值1,当
取最大值1,当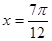 时,
时,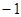 。
。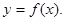
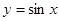 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到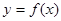 的图象?
的图象?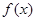 满足方程
满足方程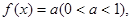 求在
求在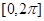 内的所有实数根之和.
内的所有实数根之和.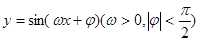 在同一个周期内,当
在同一个周期内,当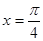 时
时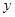 取最大值1,当
取最大值1,当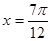 时,
时,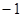 。
。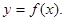
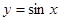 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到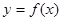 的图象?
的图象?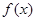 满足方程
满足方程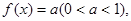 求在
求在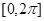 内的所有实数根之和.
内的所有实数根之和.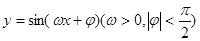 在同一个周期内,当
在同一个周期内,当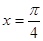 时
时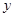 取最大值1,当
取最大值1,当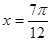 时,
时,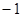 。
。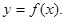
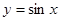 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到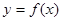 的图象?
的图象?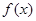 满足方程
满足方程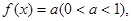 求在
求在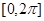 内的所有实数根之和.
内的所有实数根之和.