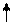题目内容
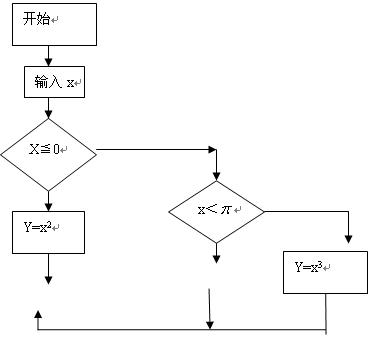
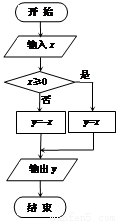
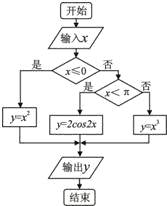 阅读流程图,若记y=f(x).
阅读流程图,若记y=f(x).
(Ⅰ) 写出y=f(x)的解析式,并求函数的值域;
(Ⅱ)若x0满足f(x0)<0 且f(f(x0))=1,求x0.
解:(I)由图可知:
该程序的作用是计算分段函数 的函数值.
的函数值.
当x≤0时,输出值y≥0时,
当0<x<π时,输出值y:-2≤y<2;
当x>π时,输出值y:y≥π3;
综上所述,函数f(x)的值域为[-2,+∞).
(Ⅱ)因为f(x0)<0,所以 <x0<
<x0< ,
,
所以,f(x0)=2cos2x0<0
所以f(f(x0))=f(2cos2x0)=(2cos2x0)2,
所以cos22x0= ,
,
所以cos2x0=- ,
,
所以x0= ,或x0=
,或x0= .
.
分析:(I)分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数 的函数值;再求此分段函数的值域;
的函数值;再求此分段函数的值域;
(Ⅱ)因为f(x0)<0,求得 <x0<
<x0< ,从而f(x0)=2cos2x0<0,f(f(x0))=f(2cos2x0)=(2cos2x0)2,解方程f(f(x0))=1,求出x0.
,从而f(x0)=2cos2x0<0,f(f(x0))=f(2cos2x0)=(2cos2x0)2,解方程f(f(x0))=1,求出x0.
点评:本小题主要考查函数单调性的应用、选择结构、分段函数的解析式求法及其图象的作法、余弦函数的定义域和值域等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
该程序的作用是计算分段函数
 的函数值.
的函数值.当x≤0时,输出值y≥0时,
当0<x<π时,输出值y:-2≤y<2;
当x>π时,输出值y:y≥π3;
综上所述,函数f(x)的值域为[-2,+∞).
(Ⅱ)因为f(x0)<0,所以
 <x0<
<x0< ,
,所以,f(x0)=2cos2x0<0
所以f(f(x0))=f(2cos2x0)=(2cos2x0)2,
所以cos22x0=
 ,
,所以cos2x0=-
 ,
,所以x0=
 ,或x0=
,或x0= .
.分析:(I)分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数
 的函数值;再求此分段函数的值域;
的函数值;再求此分段函数的值域;(Ⅱ)因为f(x0)<0,求得
 <x0<
<x0< ,从而f(x0)=2cos2x0<0,f(f(x0))=f(2cos2x0)=(2cos2x0)2,解方程f(f(x0))=1,求出x0.
,从而f(x0)=2cos2x0<0,f(f(x0))=f(2cos2x0)=(2cos2x0)2,解方程f(f(x0))=1,求出x0.点评:本小题主要考查函数单调性的应用、选择结构、分段函数的解析式求法及其图象的作法、余弦函数的定义域和值域等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
 阅读流程图,若记y=f(x).
阅读流程图,若记y=f(x).