题目内容
已知α为第二象限角,且sinα=
| ||
| 4 |
sin(α+
| ||
| sin2α+cos2α+1 |
分析:先利用两角和与差的正弦函数和二倍角公式将待求式子化成只含有角α的三角函数,再由三角函数的同角公式求出角α余弦值,从而求出结果即可.
解答:解:
=
=
,
当α为第二象限角,且sinα=
时,sinα+cosα≠0,cosα=-
,
所以
=
=-
.
sin(α+
| ||
| sin2α+cos2α+1 |
| ||||
| 2sinαcosα+2cos2α |
| ||
| 4cosα(sinα+cosα) |
当α为第二象限角,且sinα=
| ||
| 4 |
| 1 |
| 4 |
所以
sin(α+
| ||
| sin2α+cos2α+1 |
| ||
| 4cosα |
| 2 |
点评:本题主要考查了两角和与差的正弦函数、二倍角的正弦余弦、同角公式等,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 ,则2a是( )
,则2a是( ) ,
, 为第二象限角,求
为第二象限角,求 ;
; ,求
,求 的值。
的值。 ,
, 为第二象限角,求
为第二象限角,求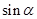 和
和 及
及 的值.
的值.