题目内容
(1)求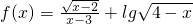 的定义域;
的定义域;
(2)求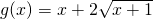 的值域.
的值域.
解:(1)欲使函数f(x)有意义,须有 ,解得2≤x<4,且x≠3,
,解得2≤x<4,且x≠3,
故函数f(x)的定义域为[2,3)∪(3,4);
(2)令t= ,则t∈[0,+∞),x=t2-1,
,则t∈[0,+∞),x=t2-1,
令h(t)=t2+2t-1=(t+1)2-2,∵h(t)在[0,+∞)上单调递增,∴h(t)≥h(0)=-1,
故函数g(x)的值域为[-1,+∞).
分析:(1)由解析法给出的函数,其定义域须满足函数解析式有意义.
(2)用换元法:令t= ,则t∈[0,+∞),从而原函数变为自变量为t的函数进行求解.
,则t∈[0,+∞),从而原函数变为自变量为t的函数进行求解.
点评:本题主要考查了函数定义域、值域的求解,对解析法给出的函数,自变量要满足解析式有意义,具有实际背景的函数应考虑实际意义;对含根号的函数值域问题,常用换元法或几何意义来解决.
 ,解得2≤x<4,且x≠3,
,解得2≤x<4,且x≠3,故函数f(x)的定义域为[2,3)∪(3,4);
(2)令t=
 ,则t∈[0,+∞),x=t2-1,
,则t∈[0,+∞),x=t2-1,令h(t)=t2+2t-1=(t+1)2-2,∵h(t)在[0,+∞)上单调递增,∴h(t)≥h(0)=-1,
故函数g(x)的值域为[-1,+∞).
分析:(1)由解析法给出的函数,其定义域须满足函数解析式有意义.
(2)用换元法:令t=
 ,则t∈[0,+∞),从而原函数变为自变量为t的函数进行求解.
,则t∈[0,+∞),从而原函数变为自变量为t的函数进行求解.点评:本题主要考查了函数定义域、值域的求解,对解析法给出的函数,自变量要满足解析式有意义,具有实际背景的函数应考虑实际意义;对含根号的函数值域问题,常用换元法或几何意义来解决.

练习册系列答案
相关题目
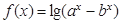 (
(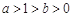 )
)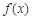 的定义域;
的定义域;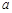 、
、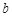 ,当
,当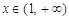 时,
时,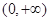 ,且
,且 若存在,求出
若存在,求出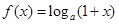 ,
,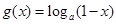 ,其中
,其中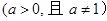 ,设
,设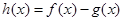 .
.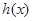 的定义域;
的定义域;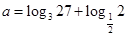 ,求使
,求使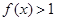 成立的
成立的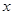 的集合.
的集合. (1)求
(1)求 的定义域;(2)求
的定义域;(2)求 (常数
(常数
 的定义域;
的定义域; 满足什么条件时,
满足什么条件时, 在
在 上恒取正值。
上恒取正值。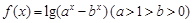 .
.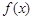 的定义域
的定义域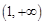 上递增且恒取正值,求
上递增且恒取正值,求 满足的关系式。
满足的关系式。