题目内容
设函数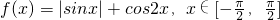 ,则函数f(x)的最小值是
,则函数f(x)的最小值是
- A.-1
- B.0
- C.

- D.

B
分析:根据x的范围把分段函数分段,配方后求出函数在两个区间段内最小值,则函数在整个定义域内的最小值可求.
解答:由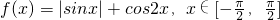 ,
,
当 时,0≤sinx≤1,
时,0≤sinx≤1,
f(x)=sinx+cos2x=-2sin2x+sinx+1=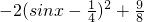 .
.
此时当sinx=1时f(x)有最小值为 ;
;
当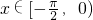 时,-1≤sinx<0,
时,-1≤sinx<0,
f(x)=-sinx+cos2x=-2sin2x-sinx+1=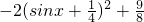 .
.
此时当sinx=-1时f(x)有最小值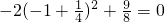 .
.
综上,函数f(x)的最小值是0.
故选B.
点评:本题考查了函数的定义域与值域,考查了分段函数值域的求法,训练了利用配方法求函数的值域,分段函数的值域是各区间段内值域的并集,此题是基础题.
分析:根据x的范围把分段函数分段,配方后求出函数在两个区间段内最小值,则函数在整个定义域内的最小值可求.
解答:由
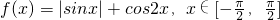 ,
,当
 时,0≤sinx≤1,
时,0≤sinx≤1,f(x)=sinx+cos2x=-2sin2x+sinx+1=
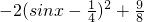 .
.此时当sinx=1时f(x)有最小值为
 ;
;当
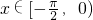 时,-1≤sinx<0,
时,-1≤sinx<0,f(x)=-sinx+cos2x=-2sin2x-sinx+1=
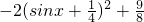 .
.此时当sinx=-1时f(x)有最小值
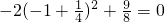 .
.综上,函数f(x)的最小值是0.
故选B.
点评:本题考查了函数的定义域与值域,考查了分段函数值域的求法,训练了利用配方法求函数的值域,分段函数的值域是各区间段内值域的并集,此题是基础题.

练习册系列答案
相关题目
 ,则函数f(x)( )
,则函数f(x)( ) ,则函数f(x)是( )
,则函数f(x)是( ) 的奇函数
的奇函数 的偶函数
的偶函数