题目内容
设a,b∈R,那么下列命题正确的是
- A.a>b?a2>b2
- B.a>|b|?a2>b2
- C.
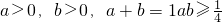
- D.
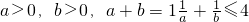
B
分析:逐个验证:A可取特值推翻结论;B利用性质可证;C、D由基本不等式求最值的方法分别可得ab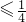 ,
, ,可得答案.
,可得答案.
解答:选项A可取a=-1,b=-2显然有a2<b2,故A不正确;
选项B由不等式可成方的性质a>|b|必有a2>b2,故B正确;
选项C由基本不等式的性质可得ab=a(1-a)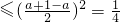 ,
,
当且仅当a=b= 时取到等号,故C错误;
时取到等号,故C错误;
选项D由a+b=1可得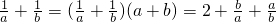
由基本不等式的性质可得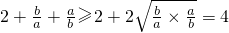 ,
,
即 ,故D错误.
,故D错误.
故选B.
点评:本题为不等式性质的应用,熟练掌握不等式的性质是解决问题的关键,属基础题.
分析:逐个验证:A可取特值推翻结论;B利用性质可证;C、D由基本不等式求最值的方法分别可得ab
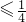 ,
, ,可得答案.
,可得答案.解答:选项A可取a=-1,b=-2显然有a2<b2,故A不正确;
选项B由不等式可成方的性质a>|b|必有a2>b2,故B正确;
选项C由基本不等式的性质可得ab=a(1-a)
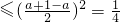 ,
,当且仅当a=b=
 时取到等号,故C错误;
时取到等号,故C错误;选项D由a+b=1可得
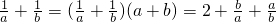
由基本不等式的性质可得
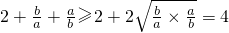 ,
,即
 ,故D错误.
,故D错误.故选B.
点评:本题为不等式性质的应用,熟练掌握不等式的性质是解决问题的关键,属基础题.

练习册系列答案
相关题目