Question

（2009江苏卷18）（本小题满分16分）

在平面直角坐标系中，已知圆和圆.

（1）若直线过点，且被圆截得的弦长为，求直线的方程；

（2）设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线和，它们分别与圆和圆相交，且直线被圆截得的弦长与直线被圆截得的弦长相等，试求所有满足条件的点P的坐标。

Answer 1

或,或。

解析:

解  (1)设直线的方程为：，即

由垂径定理，得：圆心到直线的距离，

结合点到直线距离公式，得：      

化简得：

求直线的方程为：或，即或

(2) 设点P坐标为，直线、的方程分别为：     

，即：

因为直线被圆截得的弦长与直线被圆截得的弦长相等，两圆半径相等。

由垂径定理，得：：圆心到直线与直线的距离相等。     

故有：，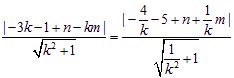

化简得：

关于的方程有无穷多解，有：           

解之得：点P坐标为或。