Question

已知向量n=(1,0),O是坐标原点,动点P满足:||比向量在n上的投影多2.

(1)求动点P的轨迹方程;

(2)设B、C是点P的轨迹上不同的两点,满足=λ(λ≠0,且λ∈R),在x轴上是否存在点A(m,0)使得⊥?若存在,求出实数m的取值范围;若不存在,说明理由.

Answer 1

解:(1)设P点的坐标为(x,y),则||=,

向量在n上的投影为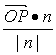=(x,y)·(1,0)=x,                    

所以=x+2.                                                    

化简得y²=4(x+1),所以动点P的轨迹方程为y²=4(x+1).                        

(2)若两点B、C满足条件=λ,得B、O、C三点共线,

设直线BC方程为x=ky,B、C两点的坐标为(x₁,y₁)、(x₂,y₂),由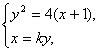得y²-4ky-4=0,

Δ=16k²+16＞0,y₁+y₂=4k,y₁y₂=-4.                                            

又⊥,所以·=0,

即(x₁-m)(x₂-m)+y₁y₂=0,                                                    

x₁x₂-m(x₁+x₂)+m²+y₁y₂=0,

所以(k²+1)y₁y₂-mk(y₁+y₂)+m²=0.

化简得(4m+4)k²=m²-4,当m=-1时不成立,                                     

当m≠-1时,

有k²=≥0.

解之,得-2≤m＜-1或m≥2.