题目内容
甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以A1,A2和A3表示由甲罐取出的球是红球,白球和黑球的事件.再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件.给出下列结论:
①P(B)=
;
②P(B|A1)=
;
③事件B与事件A1相互独立;
④A1,A2,A3是两两互斥的事件;
⑤P(B)的值不能确定,因为它与A1,A2,A3中究竟哪一个发生有关;
其中正确的有( )
①P(B)=
| 2 |
| 5 |
②P(B|A1)=
| 5 |
| 11 |
③事件B与事件A1相互独立;
④A1,A2,A3是两两互斥的事件;
⑤P(B)的值不能确定,因为它与A1,A2,A3中究竟哪一个发生有关;
其中正确的有( )
| A、②④ | B、①③ |
| C、②④⑤ | D、②③④⑤ |
分析:由题意A1,A2,A3是两两互斥的事件,由条件概率公式求出P(B|A1),P(B)=P(B|A1)+P(B|A2)+P(B|A3),对照五个命题进行判断找出正确命题,选出正确选项
解答:解:由题意A1,A2,A3是两两互斥的事件,P(A1)=
,P(A2)=
,P(A3)=
P(B|A1)=
=
=
,由此知,②正确
P(B|A2)=
,P(B|A3)=
而P(B)=P(B|A1)+P(B|A2)+P(B|A3)=
×
+
×
+
×
=
.由此知③不正确,⑤不正确
A1,A2,A3是两两互斥的事件,由此知④正确
对照四个命题知②④正确
故选A
| 5 |
| 10 |
| 2 |
| 10 |
| 3 |
| 10 |
P(B|A1)=
| P(BA1) |
| P(A1) |
| ||||
|
| 5 |
| 11 |
P(B|A2)=
| 4 |
| 11 |
| 4 |
| 11 |
而P(B)=P(B|A1)+P(B|A2)+P(B|A3)=
| 5 |
| 10 |
| 5 |
| 11 |
| 2 |
| 10 |
| 4 |
| 11 |
| 3 |
| 10 |
| 4 |
| 11 |
| 9 |
| 22 |
A1,A2,A3是两两互斥的事件,由此知④正确
对照四个命题知②④正确
故选A
点评:本题考查相互独立事件,解题的关键是理解题设中的各个事件,且熟练掌握了相互独立事件的概率简洁公式,条件概率的求法,本题较复杂,正确理解事件的内蕴是解题的突破点.

练习册系列答案
相关题目
 和
和 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以 表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。 ;
; ;[来源:]
;[来源:] 相互独立;
相互独立; 是两两互斥的事件;
是两两互斥的事件;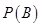 的值不能确定,因为它与
的值不能确定,因为它与 和
和 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以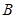 表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。 ;
;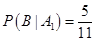 ;[来源:]
;[来源:]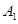 相互独立;
相互独立; 是两两互斥的事件;
是两两互斥的事件; 的值不能确定,因为它与
的值不能确定,因为它与