题目内容
已知直线(1+4k)x-(2-3k)y+(2+8k)=0(k∈R)所经过的定点F,直线l:x=-4与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.(1)求点F和圆C的方程;
(2)若直线FG与直线l交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在一点P,使得
 ?若存在,求出点P坐标;若不存在,请说明理由.
?若存在,求出点P坐标;若不存在,请说明理由.
【答案】分析:(1)直线方程分离参数,建立方程,可求F的坐标;利用左准线l与x轴的交点是圆C的圆心,确定圆心坐标,又圆C恰好经过坐标原点O,可求圆的半径,从而可求圆C的方程;
(2)求出G的坐标,进而求出FG的方程,利用点到直线的距离公式求出C(-4,0)到FG的距离,再利用勾股定理即可求出弦长的一半,进而可求解;
(3)假设存在P(s,t),G(x,y),利用两点间的距离公式化简,结合G在圆C上,即可求得结论.
解答:解:(1)将直线方程变形为:k(4x+3y+8)+(x-2y+2)=0,
令4x+3y+8=0,x-2y+2=0,解得x=-2,y=0,∴F(-2,0)
∵直线l:x=-4与x轴的交点是圆C的圆心,∴C(-4,0)
∵圆C恰好经过坐标原点O,∴r=4
∴圆C的方程为(x+4)2+y2=16;
(2)由题意G的横坐标为-3,则y= ,∴直线FG的方程为y=
,∴直线FG的方程为y=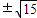 (x+2)
(x+2)
∴圆心到直线的距离为d= ,∴直线FG被圆C所截得的弦长为2
,∴直线FG被圆C所截得的弦长为2 =7;
=7;
(3)设P(s,t),G(x,y),则由 ,得
,得 =
=
整理得3(x2+y2)+(48+2s)x+2ty+144-s2-t2=0.①
又G(x,y)在圆C:(x+4)2+y2=16上,所以x2+y2+8x=0 ②
②代入①,得(2s+24)x+2ty+144-s2-t2=0.
又由G(x,y)为圆C上任意一点可知,
解得:s=-12,t=0.
所以在平面上存在一定点P,其坐标为(-12,0).
点评:本题考查圆的标准方程,考查直线与圆的位置关系,考查弦长公式,考查恒成立问题,解题的关键是假设存在,建立等式,利用恒成立的条件.
(2)求出G的坐标,进而求出FG的方程,利用点到直线的距离公式求出C(-4,0)到FG的距离,再利用勾股定理即可求出弦长的一半,进而可求解;
(3)假设存在P(s,t),G(x,y),利用两点间的距离公式化简,结合G在圆C上,即可求得结论.
解答:解:(1)将直线方程变形为:k(4x+3y+8)+(x-2y+2)=0,
令4x+3y+8=0,x-2y+2=0,解得x=-2,y=0,∴F(-2,0)
∵直线l:x=-4与x轴的交点是圆C的圆心,∴C(-4,0)
∵圆C恰好经过坐标原点O,∴r=4
∴圆C的方程为(x+4)2+y2=16;
(2)由题意G的横坐标为-3,则y=
 ,∴直线FG的方程为y=
,∴直线FG的方程为y=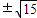 (x+2)
(x+2)∴圆心到直线的距离为d=
 ,∴直线FG被圆C所截得的弦长为2
,∴直线FG被圆C所截得的弦长为2 =7;
=7;(3)设P(s,t),G(x,y),则由
 ,得
,得 =
=
整理得3(x2+y2)+(48+2s)x+2ty+144-s2-t2=0.①
又G(x,y)在圆C:(x+4)2+y2=16上,所以x2+y2+8x=0 ②
②代入①,得(2s+24)x+2ty+144-s2-t2=0.
又由G(x,y)为圆C上任意一点可知,

解得:s=-12,t=0.
所以在平面上存在一定点P,其坐标为(-12,0).
点评:本题考查圆的标准方程,考查直线与圆的位置关系,考查弦长公式,考查恒成立问题,解题的关键是假设存在,建立等式,利用恒成立的条件.

练习册系列答案
相关题目
