题目内容
某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如下关系:
(1)画出散点图,并判断y与x是否具有线性相关关系?
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.
(1)见解析 (2)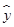 =-3x+161.5 (3) 销售单价为42元时,能获得最大日销售利润
=-3x+161.5 (3) 销售单价为42元时,能获得最大日销售利润
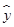 =-3x+161.5 (3) 销售单价为42元时,能获得最大日销售利润
=-3x+161.5 (3) 销售单价为42元时,能获得最大日销售利润解:(1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.
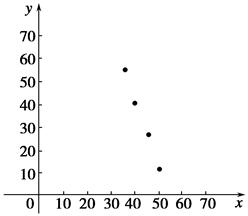
(2)∵
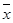 =
=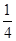 ×(35+40+45+50)=42.5.
×(35+40+45+50)=42.5.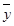 =
=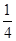 ×(56+41+28+11)=34.
×(56+41+28+11)=34.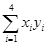 =35×56+40×41+45×28+50×11=5 410.
=35×56+40×41+45×28+50×11=5 410. =352+402+452+502=7 350.
=352+402+452+502=7 350.∴
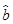 =
=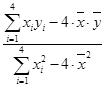 =
=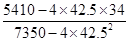 =
=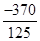 ≈-3.
≈-3.∴
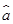 =
=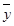 -
-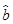
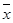 =34-(-3)×42.5=161.5.
=34-(-3)×42.5=161.5.∴
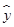 =-3x+161.5.
=-3x+161.5.(3)依题意有
P=(-3x+161.5)(x-30)=-3x2+251.5x-4 845
=-3(x-
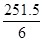 )2+
)2+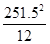 -4 845.
-4 845.∴当x=
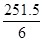 ≈42时,P有最大值,约为426.
≈42时,P有最大值,约为426.即预测销售单价为42元时,能获得最大日销售利润.
方法点评:该题属于线性回归问题,解答本类题目的关键首先应先通过散点图(或相关性检验求相关系数r)来分析两变量间的关系是否相关,然后再利用求回归方程的公式求解回归方程,在此基础上,借助回归方程对实际问题进行分析.

练习册系列答案
相关题目
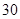 天)的空气质量指数
天)的空气质量指数 监测数据,统计结果如下:
监测数据,统计结果如下:









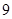

 (单位:元)与空气质量指数
(单位:元)与空气质量指数 )的
)的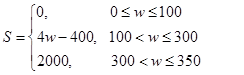
 元且不超过
元且不超过 元的概率.
元的概率.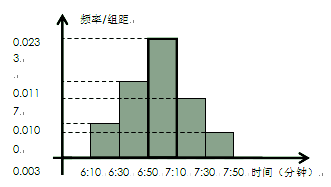
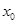 ;
;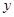 在上午
在上午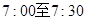 之间,而送报人每天在
之间,而送报人每天在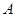 )的概率;
)的概率;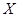 的数学期望.
的数学期望.
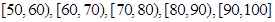 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 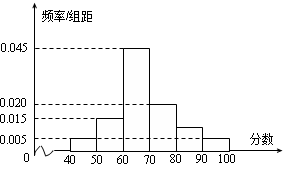
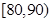 的频率;
的频率; 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )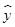 =0.50x-0.81,则x=25时,
=0.50x-0.81,则x=25时,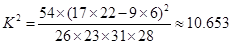 ,因为
,因为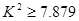 ,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为_ .
,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为_ .