题目内容
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.(Ⅰ)求第n年初M的价值an的表达式;
(Ⅱ)设An=
| a1+a2+…+an | n |
分析:(I)通过对n的分段讨论,得到一个等差数列和一个等比数列,利用等差数列的通项公式及等比数列的通项公式求出第n年初M的价值an的表达式;
(II)利用等差数列、等比数列的前n项和公式求出An,判断出其两段的单调性,求出两段的最小值,与80比较,判断出须在第9年初对M更新.
(II)利用等差数列、等比数列的前n项和公式求出An,判断出其两段的单调性,求出两段的最小值,与80比较,判断出须在第9年初对M更新.
解答:解:(I)当n<6时,数列{an}是首项为120,公差为-10的等差数列
an=120-10(n-1)=130-10n
当n≥6时,数列{an}是以a6为首项,公比为
的等比数列,又a6=70
所以an=70×(
)n-6
因此,第n年初,M的价值an的表达式为an=
(II)设Sn表示数列{an}的前n项和,由等差、等比数列的求和公式得
当1≤n≤6时,Sn=120n-5n(n-1),An=120-5(n-1)=125-5n
当n≥7时,由于S6=570故
Sn=S6+(a7+a8+…+an)=570+
=780-210×(
)n-6An=
因为{an}是递减数列,
所以{An}是递减数列,
又A8=
=82
>80
A9=
=76
<80
所以须在第9年初对M更新.
an=120-10(n-1)=130-10n
当n≥6时,数列{an}是以a6为首项,公比为
| 3 |
| 4 |
所以an=70×(
| 3 |
| 4 |
因此,第n年初,M的价值an的表达式为an=
|
(II)设Sn表示数列{an}的前n项和,由等差、等比数列的求和公式得
当1≤n≤6时,Sn=120n-5n(n-1),An=120-5(n-1)=125-5n
当n≥7时,由于S6=570故
Sn=S6+(a7+a8+…+an)=570+
70×
| ||||
1-
|
| 3 |
| 4 |
780-210×(
| ||
| n |
因为{an}是递减数列,
所以{An}是递减数列,
又A8=
780-210×(
| ||
| 8 |
| 47 |
| 64 |
A9=
780-210×(
| ||
| 9 |
| 79 |
| 96 |
所以须在第9年初对M更新.
点评:本题考查等差数列的通项公式,前n项和公式、考查等比数列的通项公式及前n项和公式、考查分段函数的问题要分到研究.

练习册系列答案
相关题目
 的表达式;
的表达式; 若
若 大于80万元,则M继续使用,否则须在第n年初对M更新,
大于80万元,则M继续使用,否则须在第n年初对M更新,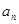 的表达式;
的表达式;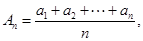 若
若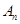 大于80万元,则M继续使用,否则须在第n年初对M更新,证明:须在第9年初对M更新.
大于80万元,则M继续使用,否则须在第n年初对M更新,证明:须在第9年初对M更新.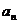 的表达式;
的表达式;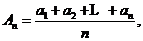 若
若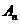 大于80万元,则M继续使用,否则须在第n年初对M更新,证明:须在第9年初对M更新.
大于80万元,则M继续使用,否则须在第n年初对M更新,证明:须在第9年初对M更新.