题目内容

(1)
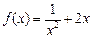 (x>0)
(x>0)(2)不存在实数a使得g(x)为奇函数
(3){ x|0<x<1或
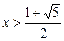
(1)∵ 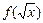 =
=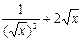 , ∴
, ∴ 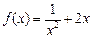 (x>0).……… 3分
(x>0).……… 3分
(2)∵ g(x)=" ax2" + 2x 的定义域为(0,+∞).
∵ g(1)=" 2" + a,g(-1)不存在,∴ g(1)≠-g(-1),
∴ 不存在实数a使得g(x)为奇函数.…………………… 5分
(3)∵ f(x)-x>2, ∴ f(x)-x-2>0,
即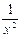 + x-2>0,有x3-2x2 + 1>0,
+ x-2>0,有x3-2x2 + 1>0,
于是(x3-x2)-(x2-1)>0,∴ x2(x-1)-(x-1)(x + 1)>0,
∴(x-1)(x2-x-1)>0, ∴ (x-1)(x-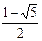 )(x-
)(x-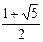 )>0,
)>0,
∴ 结合x>0得0<x<1或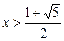 .
.
因此原不等式的解集为 { x|0<x<1或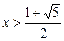
 . ……………… 12分
. ……………… 12分
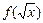 =
=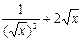 , ∴
, ∴ 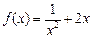 (x>0).……… 3分
(x>0).……… 3分(2)∵ g(x)=" ax2" + 2x 的定义域为(0,+∞).
∵ g(1)=" 2" + a,g(-1)不存在,∴ g(1)≠-g(-1),
∴ 不存在实数a使得g(x)为奇函数.…………………… 5分
(3)∵ f(x)-x>2, ∴ f(x)-x-2>0,
即
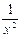 + x-2>0,有x3-2x2 + 1>0,
+ x-2>0,有x3-2x2 + 1>0,于是(x3-x2)-(x2-1)>0,∴ x2(x-1)-(x-1)(x + 1)>0,
∴(x-1)(x2-x-1)>0, ∴ (x-1)(x-
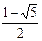 )(x-
)(x-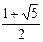 )>0,
)>0,∴ 结合x>0得0<x<1或
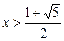 .
.因此原不等式的解集为 { x|0<x<1或
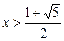
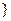 . ……………… 12分
. ……………… 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
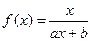 (
(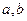 为常数,
为常数,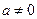 ),满足
),满足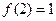 ,且
,且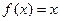 有两个相同的解。
有两个相同的解。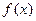 的表达式;
的表达式;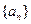 满足
满足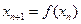 ,且
,且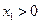 ,求证:数列
,求证:数列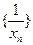 是等差数列。
是等差数列。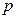 :方程
:方程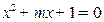 有两个不相等的实根;
有两个不相等的实根; :不等式
:不等式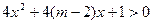 的解集为
的解集为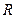 ;
;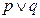 为真,
为真,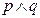 为假,求实数
为假,求实数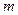 的取值范围。
的取值范围。 的最小值为
的最小值为 .
.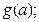
 求
求 及此时
及此时 的最大值.(12分)
的最大值.(12分) 是
是 上的奇函数,且
上的奇函数,且 ,当
,当 时,
时, ,则
,则 ="( " )
="( " ) )=
)=  在区间[1,2]上都是减函数,则a的取值范围是( )
在区间[1,2]上都是减函数,则a的取值范围是( ) 的值域是
的值域是



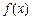 满足:①定义域为
满足:①定义域为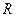 ;②对任意
;②对任意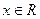 ,有
,有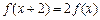 ;③当
;③当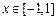 时,
时,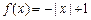 .则方程
.则方程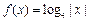 在区间
在区间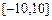 内的解的个数是( )
内的解的个数是( ) (x)过点(-1,1),且g(x)
(x)过点(-1,1),且g(x) =f(x-1),则f(7)+f(8)的值为__▲____.
=f(x-1),则f(7)+f(8)的值为__▲____.