题目内容
设![]() 是正数组成的数列,其前n项和为Sn,且对于所有正整数n,有
是正数组成的数列,其前n项和为Sn,且对于所有正整数n,有![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]()
(1)解:∵![]() ①
①
∴![]() ②
②
②―①得
![]() ,化简得:
,化简得:
![]()
∵![]() ∴
∴![]()
∴![]() 又∵
又∵![]()
∴数列![]() 是以首项为1,公差为2的等差数列。
是以首项为1,公差为2的等差数列。
∴通项公式为![]()
(2)证明:∵![]()
![]() 。
。
∴![]() ①
①
![]() ②
②
①―②得:
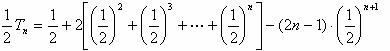
![]()
∴![]()
令![]()
∵![]()
![]()
![]()
∵数列![]() 递增, ∴
递增, ∴![]()
故![]() 成立。
成立。

练习册系列答案
相关题目
题目内容
设![]() 是正数组成的数列,其前n项和为Sn,且对于所有正整数n,有
是正数组成的数列,其前n项和为Sn,且对于所有正整数n,有![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]()
(1)解:∵![]() ①
①
∴![]() ②
②
②―①得
![]() ,化简得:
,化简得:
![]()
∵![]() ∴
∴![]()
∴![]() 又∵
又∵![]()
∴数列![]() 是以首项为1,公差为2的等差数列。
是以首项为1,公差为2的等差数列。
∴通项公式为![]()
(2)证明:∵![]()
![]() 。
。
∴![]() ①
①
![]() ②
②
①―②得:
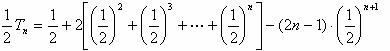
![]()
∴![]()
令![]()
∵![]()
![]()
![]()
∵数列![]() 递增, ∴
递增, ∴![]()
故![]() 成立。
成立。
