题目内容
不等式(x2-1)(x2-6x+8)≥0的解集是
- A.{x|x≤-1}∪{x|x≥4}
- B.{x|1≤x≤2}∪{x|x≥4}
- C.{x|x≤-1}∪{x|1≤x≤2}
- D.{x|x≤-1或1≤x≤2或x≥4}
D
分析:先把原不等式转化为(x-1)(x+1)(x-2)(x-4)≥0;再借助于数轴标根法画出图象 即可得出结论.
解答: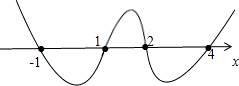 解:原不等式转化为:(x-1)(x+1)(x-2)(x-4)≥0.
解:原不等式转化为:(x-1)(x+1)(x-2)(x-4)≥0.
借助于数轴标根法可得:x≤-1或1≤x≤2或x≥4
故选:D.
点评:本题主要考查不等式的解法.在解高次不等式时,一般是先对其因式分解,分解为一次因式相乘的形式(一次项系数为正);再把根标在数轴上,根据图象即可得出结论.
分析:先把原不等式转化为(x-1)(x+1)(x-2)(x-4)≥0;再借助于数轴标根法画出图象 即可得出结论.
解答:
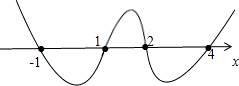 解:原不等式转化为:(x-1)(x+1)(x-2)(x-4)≥0.
解:原不等式转化为:(x-1)(x+1)(x-2)(x-4)≥0.借助于数轴标根法可得:x≤-1或1≤x≤2或x≥4
故选:D.
点评:本题主要考查不等式的解法.在解高次不等式时,一般是先对其因式分解,分解为一次因式相乘的形式(一次项系数为正);再把根标在数轴上,根据图象即可得出结论.

练习册系列答案
相关题目