Question

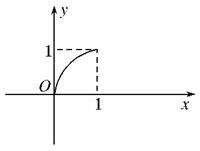
在区间[0,1]上给定曲线y＝x²，如图所示，试在此区间内确定t的值，使图中的阴影部分的面积S₁与S₂之和最小.

Answer 1

面积S₁等于边长为t与t²的矩形的面积去掉曲线y＝x²与x轴、直线x＝t围成的面积，即面积S₂等于曲线y＝x²与x轴、x＝t，x＝1围成的面积去掉矩形面积，矩形边长分别为t²，(1－t)，即S₂＝

所以阴影部分面积,由S′(t)＝4t²－2t＝4t(t－)＝0，得t＝0或t＝.经验证知，当t＝时，S最小.