题目内容
(1)
已知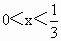 ,求函数y=x(1-3x)的最大值.
,求函数y=x(1-3x)的最大值.
(2)
求函数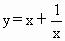 的值域.
的值域.
答案:略
解析:
解析:
|
第 (1)题,求函数的最大值,由极值定理可知,需构造某个和为定值,可考虑把括号内外x的系数变成互为相反数即可;第(2)题中,未指出x>0,因而不能直接使用基本不等式,需分x>0与x<0讨论.(1) 解法1:∵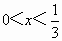 ,∴ ,∴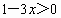 . .
∴  ,当且仅当3x=1-3x,即 ,当且仅当3x=1-3x,即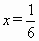 时,等号成立.∴当 时,等号成立.∴当 时,函数取最大值 时,函数取最大值 . .
解法 2:∵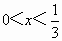 ,∴ ,∴ . .
∴  ,当且仅当 ,当且仅当 ,即 ,即 时,等号成立.∴ 时,等号成立.∴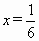 时,函数取最大值 时,函数取最大值 . .
本小题也可以将解析式展开,使用二次函数配方法求配,使用基本不等式求积的最大值,关键是构造某个和为定值,为使用基本不等式创造条件,同时要注意等号成立的条件是否具备. (2) 解:当x>0时,由基本不等式,得 当且仅当x=1时,等号成立; 当且仅当x=1时,等号成立;
当 x<0时, . .
∵- x>0,∴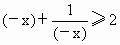 ,当且仅当 ,当且仅当 ,即x=-1时,等号成立. ,即x=-1时,等号成立.
∴  . .
综上可知:函数  的值域为 的值域为 . .
在利用基本不等式求最值 (或值域)时,要注意“一正二定三相等”是否同时具备,否则所求结果可能出错. |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
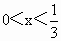 ,求函数y=x(1-3x)的最大值.
,求函数y=x(1-3x)的最大值.
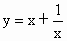 的值域.
的值域.
 ,求函数y=x(1-3x)的最大值.
,求函数y=x(1-3x)的最大值.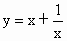 的值域.
的值域.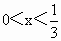 ,求函数y=x(1-3x)的最大值.
,求函数y=x(1-3x)的最大值. 的值域.
的值域.