题目内容
“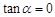 ,且
,且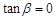 ”是“
”是“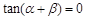 ”成立的 ▲ 条件.(在“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”中选填一种)
”成立的 ▲ 条件.(在“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”中选填一种)
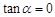 ,且
,且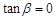 ”是“
”是“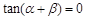 ”成立的 ▲ 条件.(在“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”中选填一种)
”成立的 ▲ 条件.(在“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”中选填一种)充分不必要
分析:利用两个角的和的正切公式得到若“tanα=0,且tanβ=0”成立,“tan(α+β)=0”一定成立;反之,通过举反例得到若“tan(α+β)=0”成立,“tanα=0,且tanβ=0”不成立,利用充要条件的有关定义得到结论.
解:若“tanα=0,且tanβ=0”成立,则有tan(α+β)= =0,所以“tan(α+β)=0”成立;
=0,所以“tan(α+β)=0”成立;
反之,若“tan(α+β)=0”成立,例如α= ,β=
,β=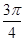
满足tan(α+β)=0但“tanα=0,且tanβ=0”不成立,
所以“tanα=0,且tanβ=0”是“tan(α+β)=0”成立的充分不必要条件.
故答案为:充分不必要.
点评:本题考查判断一个条件是另一个条件的什么条件,应该两边互相推一下,然后利用充要条件的有关定义进行判断即可
解:若“tanα=0,且tanβ=0”成立,则有tan(α+β)=
 =0,所以“tan(α+β)=0”成立;
=0,所以“tan(α+β)=0”成立;反之,若“tan(α+β)=0”成立,例如α=
 ,β=
,β=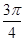
满足tan(α+β)=0但“tanα=0,且tanβ=0”不成立,
所以“tanα=0,且tanβ=0”是“tan(α+β)=0”成立的充分不必要条件.
故答案为:充分不必要.
点评:本题考查判断一个条件是另一个条件的什么条件,应该两边互相推一下,然后利用充要条件的有关定义进行判断即可

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 成立的充分不必要条件是( )
成立的充分不必要条件是( )
 或
或

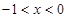 或
或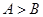 ”是“
”是“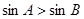 ”的
”的 x∈R,使得x2-x>0”的否定是“
x∈R,使得x2-x>0”的否定是“ x∈R,x2-x<0”
x∈R,x2-x<0” =(2,2)
=(2,2)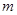 、
、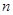 为两条不同的直线,
为两条不同的直线,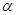 、
、 为两个不同的平面,且
为两个不同的平面,且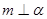 ,
,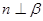 ,
,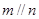 ,则
,则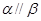 ②若
②若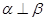 ,则
,则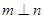
 则“
则“ 且
且 ”是“
”是“ ”的
”的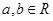 ,则“
,则“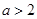 且
且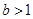 ”是“
”是“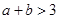 且
且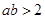 ”的( )
”的( )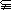 B”;
B”;