题目内容
圆台的轴截面面积是Q,母线与下底面成60°角,则圆台的内切球的表面积是( )。
A. | B. Q Q | C. Q Q | D. Q Q |
D
解析考点:球的体积和表面积.
分析:画出图形,设上底半径为a,下底半径为b,高为h,母线长为l,在轴截面(梯形)内作内切加圆,根据条件母线与上下底面半径的关系,母线与下底面成60°,圆台的轴截面面积,列出方程,求出内切球的半径,求出表面积即可.
解答: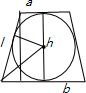
解:设上底半径为a,下底半径为b,高为h,母线长为l,
在轴截面(梯形)内作内切加圆,
可知该梯形的斜边(母线)为两底半径之和,
即:l="b+a" ①
依条件 母线与下底面成60°,∴l=2(b-a) ②
h=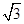 (b-a) ③
(b-a) ③
依条件 圆台的轴截面面积是Q知:(b+a)h="Q" ④
由:①②得:b+a=2(b-a) 代入④得:2(b-a)h="Q" 与③相乘得:h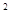 =
=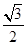 Q
Q
再由球表面积公式得 S=4π(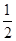 h)
h)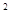 =πh
=πh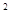
∴所求球表面积为 S=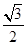 πQ
πQ
故选D
点评:本题是基础题,考查圆台的内切球的有关知识,注意轴截面图形的应用,圆的切线的应用,是本题的突破口.考查空间想象能力

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
某几何体的三视图及尺寸如图示,则该几何体的表面积为 ( )
A. | B. | C. | D.  |
下列说法正确的是
| A.平行投影的投影线相交于一点,中心投影的投影线相交于一点 |
| B.平行投影的投影线相交于一点,中心投影的投影线互相平行 |
| C.平行投影的投影线互相平行,中心投影的投影线互相平行 |
| D.平行投影的投影线互相平行,中心投影的投影线相交于一点 |
如图是某一几何体的三视图,则这个几何体的体积为( ) 
| A.4 | B.8 | C.16 | D.20 |
正方体的表面积是a2,它的顶点都在一个球面上,则这个球的表面积是
( )
| A. | B. |
| C.2πa2 | D.3πa2 |
 的正方形,主视图与左视图是边长为
的正方形,主视图与左视图是边长为



 (1)(3)
(1)(3)  (2)(4)
(2)(4)  (3)(4)
(3)(4)  (1)(2)
(1)(2)





 中,若
中,若 ,
, ,则点
,则点 到平面
到平面 的距离为( )
的距离为( )
 B
B .
.  C.
C.  D.
D. 