题目内容
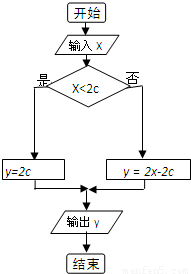
已知常数c>0.根据如图的程序框图:
(1)写出y与x得函数关系式y=f(x);
(2)设p:函数y=c3x+1在R上单调递减;q:不等式f(x)>1的解集为R,如果p或q为真,p且q为假,求c的取值范围.
(1)写出y与x得函数关系式y=f(x);
(2)设p:函数y=c3x+1在R上单调递减;q:不等式f(x)>1的解集为R,如果p或q为真,p且q为假,求c的取值范围.
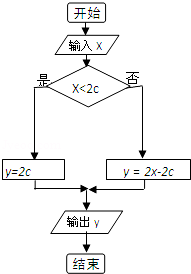
解:(1)根据流程图可知是条件结构
算法执行到判断框给定的条件P是否成立,选择不同的执行框(A框、B框),
故可用分段函数表示y=f(x)=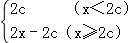
(2)命题p?0<c<1,又∵c>0∴¬p?c≥1
又∵x<2c时,f(x)=2c;
x≥2c时,f(x)=2x﹣2c≥2c
∴f(x)min=2c
∴命题q:不等式f(x)>1的解集为R?2c>1?c>
∴¬q?0<c≤
又由已知:p或q为真,p且q为假,则p、q必一真一假.
∴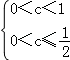 或者
或者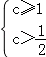
?0<c≤ 或者c≥1
或者c≥1
算法执行到判断框给定的条件P是否成立,选择不同的执行框(A框、B框),
故可用分段函数表示y=f(x)=
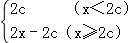
(2)命题p?0<c<1,又∵c>0∴¬p?c≥1
又∵x<2c时,f(x)=2c;
x≥2c时,f(x)=2x﹣2c≥2c
∴f(x)min=2c
∴命题q:不等式f(x)>1的解集为R?2c>1?c>

∴¬q?0<c≤

又由已知:p或q为真,p且q为假,则p、q必一真一假.
∴
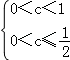 或者
或者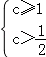
?0<c≤
 或者c≥1
或者c≥1
练习册系列答案
相关题目
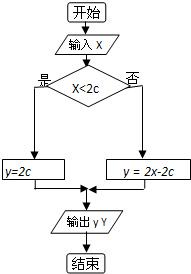 已知常数c>0根据如图的程序框图:写出y与x得函数关系式y=f(x).
已知常数c>0根据如图的程序框图:写出y与x得函数关系式y=f(x). 已知常数c>0.根据如图的程序框图:
已知常数c>0.根据如图的程序框图: 已知常数c>0根据如图的程序框图:写出y与x得函数关系式y=f(x).
已知常数c>0根据如图的程序框图:写出y与x得函数关系式y=f(x).