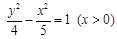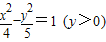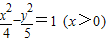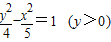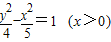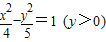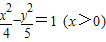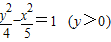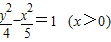题目内容
已知点F1(-3,0)和F2(3,0),动点P到F1、F2的距离之差为4,则点P的轨迹方程为( )
分析:由题设知点P的轨迹方程是焦点在x轴正半轴的双曲线的右支,设其方程为
-
=1,由题设知c=3,a=2,由此能出点P的轨迹方程.
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:由题设知点P的轨迹方程是焦点在x轴正半轴的双曲线的右支,
设其方程为
-
=1(x>0)(a>0,b>0),
由题设知c=3,a=2,b2=9-4=5,
∴点P的轨迹方程为
-
=1(x>0).
故选B.
设其方程为
| x2 |
| a2 |
| y2 |
| b2 |
由题设知c=3,a=2,b2=9-4=5,
∴点P的轨迹方程为
| x2 |
| 4 |
| y2 |
| 5 |
故选B.
点评:本题考查点P的轨迹方程的求法,解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
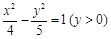 B.
B.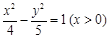
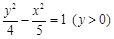 D.
D.