题目内容
定义运算“*”,对于n∈N*,满足以下运算性质:①1*1=1 ②(n+1)*1=3(n*1),则f(n)=n*1的表达式为f(n)=
3n-1
3n-1
.分析:根据定义中的运算法则,可得
=3,f(1)=1,从而f(n)构成以1为首项,3为公比的等比数列,故可求.
| f(n+1) |
| f(n) |
解答:解:由题意,
=3,f(1)=1
∴f(n)构成以1为首项,3为公比的等比数列
∴f(n)=3n-1
故答案为3n-1
| f(n+1) |
| f(n) |
∴f(n)构成以1为首项,3为公比的等比数列
∴f(n)=3n-1
故答案为3n-1
点评:本题题型是给出新的运算利用运算性质进行求值,主要抓住运算的本质,改变式子中字母的值再反复运算性质求出值,考查了观察能力和分析、解决问题的能力

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 ,第1小题满分4分,第2小题满分6分、第3小题满分6分.
,第1小题满分4分,第2小题满分6分、第3小题满分6分.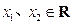 ,常数
,常数 ,定义运算“
,定义运算“ ”:
”: ,定义运算“
,定义运算“ ”:
”: ;对于两点
;对于两点 、
、 ,定义
,定义 .
. ,求动点
,求动点 的轨迹
的轨迹 ;
; 与(1)中轨迹
与(1)中轨迹 ,试求
,试求
 的值;
的值; 不过原点且与
不过原点且与 轴交于点S,与
轴交于点S,与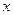 轴交于点T,并且与(1)中轨迹
轴交于点T,并且与(1)中轨迹 的取值范围.
的取值范围.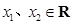 ,常数
,常数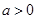 ,定义运算“
,定义运算“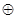 ”:
”: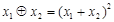 ,定义运算“
,定义运算“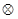 ”:
”: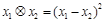 ;对于两点
;对于两点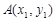 、
、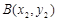 ,定义
,定义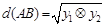 .
.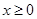 ,求动点
,求动点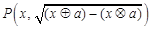 的轨迹
的轨迹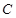 ;
;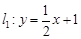 与(1)中轨迹
与(1)中轨迹 ,试求
,试求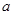 的值;
的值;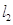 不过原点且与
不过原点且与 轴交于点S,与
轴交于点S,与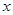 轴交于点T,并且与(1)中轨迹
轴交于点T,并且与(1)中轨迹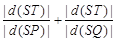 的取值范围.
的取值范围.