题目内容
如下图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C为圆周上不同于A、B的一点.
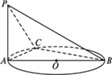
(1)当点C在圆周上运动时,问二面角A-PC-B的大小是否随之而变化?并证明你的结论.
(2)过圆心O如何作平面PBC的垂线?试研究垂足的位置,并证明你的结论.
答案:
解析:
解析:
|
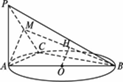
解:(1)不变化, ∵PA⊥平面ABC, ∴PA⊥BC. 又∵BC⊥AC,AC∩BC=C, ∴BC⊥平面PAC. ∴平面PAC⊥平面PBC. ∴二面角A-PC-B总是直二面角,它的大小不随点M位置的变化而变化. (2)如下图,过A作PC的垂线PM,垂足为M,连结BM,过点O作BM的垂线OH,则点H就是所求.
∵平面PAC⊥平面PBC,AM⊥PC. ∴平面ABM⊥平面PBC. 又∵OH⊥BM,∴OH⊥平面PBC. |

练习册系列答案
相关题目

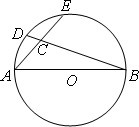
 如下图,AC是⊙O的直径,B是圆上一点,∠ABC的平分线与⊙O相交于D,已知BC=1,AB=
如下图,AC是⊙O的直径,B是圆上一点,∠ABC的平分线与⊙O相交于D,已知BC=1,AB=